Machine Learning's Dropout Training is Distributionally Robust Optimal
Paper and Code
Sep 13, 2020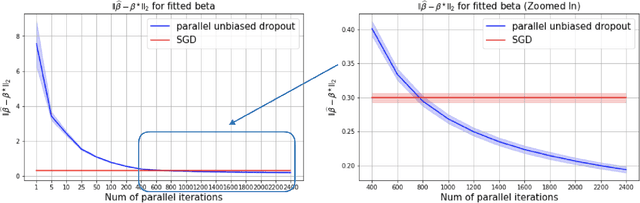

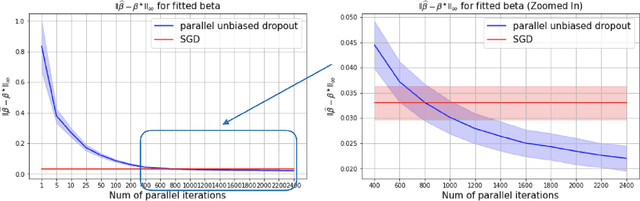

This paper shows that dropout training in Generalized Linear Models is the minimax solution of a two-player, zero-sum game where an adversarial nature corrupts a statistician's covariates using a multiplicative nonparametric errors-in-variables model. In this game---known as a Distributionally Robust Optimization problem---nature's least favorable distribution is dropout noise, where nature independently deletes entries of the covariate vector with some fixed probability $\delta$. Our decision-theoretic analysis shows that dropout training---the statistician's minimax strategy in the game---indeed provides out-of-sample expected loss guarantees for distributions that arise from multiplicative perturbations of in-sample data. This paper also provides a novel, parallelizable, Unbiased Multi-Level Monte Carlo algorithm to speed-up the implementation of dropout training. Our algorithm has a much smaller computational cost compared to the naive implementation of dropout, provided the number of data points is much smaller than the dimension of the covariate vector.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge