Self Normalizing Flows

Efficient gradient computation of the Jacobian determinant term is a core problem of the normalizing flow framework. Thus, most proposed flow models either restrict to a function class with easy evaluation of the Jacobian determinant, or an efficient estimator thereof. However, these restrictions limit the performance of such density models, frequently requiring significant depth to reach desired performance levels. In this work, we propose Self Normalizing Flows, a flexible framework for training normalizing flows by replacing expensive terms in the gradient by learned approximate inverses at each layer. This reduces the computational complexity of each layer's exact update from $\mathcal{O}(D^3)$ to $\mathcal{O}(D^2)$, allowing for the training of flow architectures which were otherwise computationally infeasible, while also providing efficient sampling. We show experimentally that such models are remarkably stable and optimize to similar data likelihood values as their exact gradient counterparts, while surpassing the performance of their functionally constrained counterparts.

Integer Discrete Flows and Lossless Compression

Lossless compression methods shorten the expected representation size of data without loss of information, using a statistical model. Flow-based models are attractive in this setting because they admit exact likelihood optimization, which is equivalent to minimizing the expected number of bits per message. However, conventional flows assume continuous data, which may lead to reconstruction errors when quantized for compression. For that reason, we introduce a flow-based generative model for ordinal discrete data called Integer Discrete Flow (IDF): a bijective integer map that can learn rich transformations on high-dimensional data. As building blocks for IDFs, we introduce a flexible transformation layer called integer discrete coupling. Our experiments show that IDFs are competitive with other flow-based generative models. Furthermore, we demonstrate that IDF based compression achieves state-of-the-art lossless compression rates on CIFAR10, ImageNet32, and ImageNet64. To the best of our knowledge, this is the first lossless compression method that uses invertible neural networks.

Probabilistic Binary Neural Networks

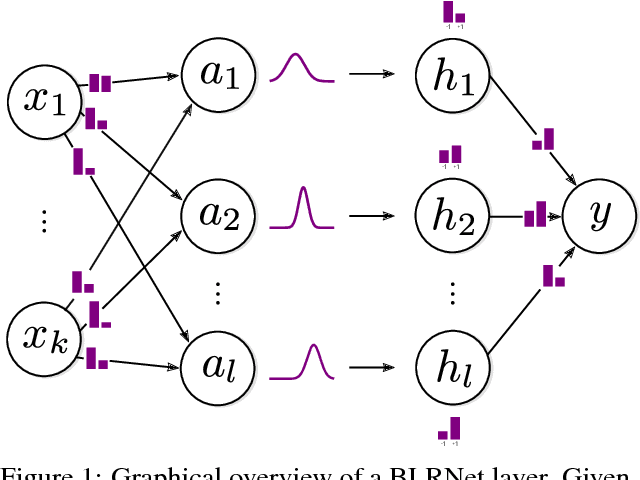
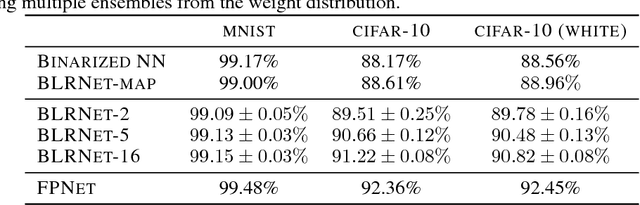
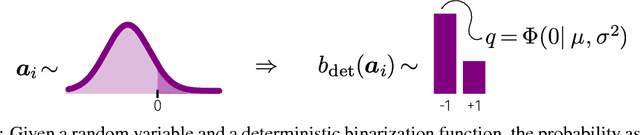
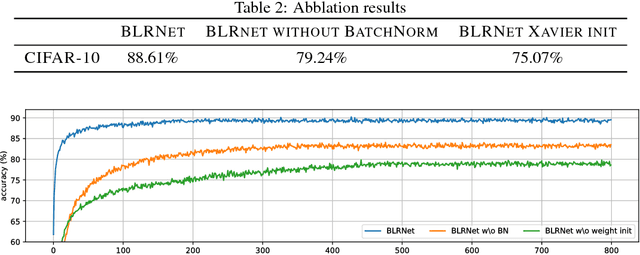
Low bit-width weights and activations are an effective way of combating the increasing need for both memory and compute power of Deep Neural Networks. In this work, we present a probabilistic training method for Neural Network with both binary weights and activations, called BLRNet. By embracing stochasticity during training, we circumvent the need to approximate the gradient of non-differentiable functions such as sign(), while still obtaining a fully Binary Neural Network at test time. Moreover, it allows for anytime ensemble predictions for improved performance and uncertainty estimates by sampling from the weight distribution. Since all operations in a layer of the BLRNet operate on random variables, we introduce stochastic versions of Batch Normalization and max pooling, which transfer well to a deterministic network at test time. We evaluate the BLRNet on multiple standardized benchmarks.

HexaConv

The effectiveness of Convolutional Neural Networks stems in large part from their ability to exploit the translation invariance that is inherent in many learning problems. Recently, it was shown that CNNs can exploit other invariances, such as rotation invariance, by using group convolutions instead of planar convolutions. However, for reasons of performance and ease of implementation, it has been necessary to limit the group convolution to transformations that can be applied to the filters without interpolation. Thus, for images with square pixels, only integer translations, rotations by multiples of 90 degrees, and reflections are admissible. Whereas the square tiling provides a 4-fold rotational symmetry, a hexagonal tiling of the plane has a 6-fold rotational symmetry. In this paper we show how one can efficiently implement planar convolution and group convolution over hexagonal lattices, by re-using existing highly optimized convolution routines. We find that, due to the reduced anisotropy of hexagonal filters, planar HexaConv provides better accuracy than planar convolution with square filters, given a fixed parameter budget. Furthermore, we find that the increased degree of symmetry of the hexagonal grid increases the effectiveness of group convolutions, by allowing for more parameter sharing. We show that our method significantly outperforms conventional CNNs on the AID aerial scene classification dataset, even outperforming ImageNet pre-trained models.