Early Failure Detection in Autonomous Surgical Soft-Tissue Manipulation via Uncertainty Quantification

Autonomous surgical robots are a promising solution to the increasing demand for surgery amid a shortage of surgeons. Recent work has proposed learning-based approaches for the autonomous manipulation of soft tissue. However, due to variability in tissue geometries and stiffnesses, these methods do not always perform optimally, especially in out-of-distribution settings. We propose, develop, and test the first application of uncertainty quantification to learned surgical soft-tissue manipulation policies as an early identification system for task failures. We analyze two different methods of uncertainty quantification, deep ensembles and Monte Carlo dropout, and find that deep ensembles provide a stronger signal of future task success or failure. We validate our approach using the physical daVinci Research Kit (dVRK) surgical robot to perform physical soft-tissue manipulation. We show that we are able to successfully detect task failure and request human intervention when necessary while still enabling autonomous manipulation when possible. Our learned tissue manipulation policy with uncertainty-based early failure detection achieves a zero-shot sim2real performance improvement of 47.5% over the prior state of the art in learned soft-tissue manipulation. We also show that our method generalizes well to new types of tissue as well as to a bimanual soft tissue manipulation task.

Modeling Kinematic Uncertainty of Tendon-Driven Continuum Robots via Mixture Density Networks

Tendon-driven continuum robot kinematic models are frequently computationally expensive, inaccurate due to unmodeled effects, or both. In particular, unmodeled effects produce uncertainties that arise during the robot's operation that lead to variability in the resulting geometry. We propose a novel solution to these issues through the development of a Gaussian mixture kinematic model. We train a mixture density network to output a Gaussian mixture model representation of the robot geometry given the current tendon displacements. This model computes a probability distribution that is more representative of the true distribution of geometries at a given configuration than a model that outputs a single geometry, while also reducing the computation time. We demonstrate one use of this model through a trajectory optimization method that explicitly reasons about the workspace uncertainty to minimize the probability of collision.

Accounting for Hysteresis in the Forward Kinematics of Nonlinearly-Routed Tendon-Driven Continuum Robots via a Learned Deep Decoder Network

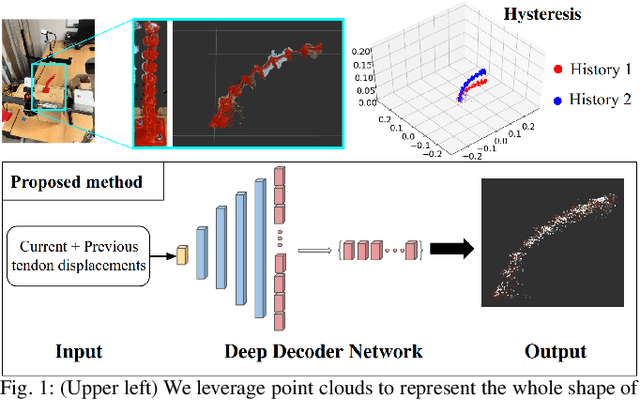
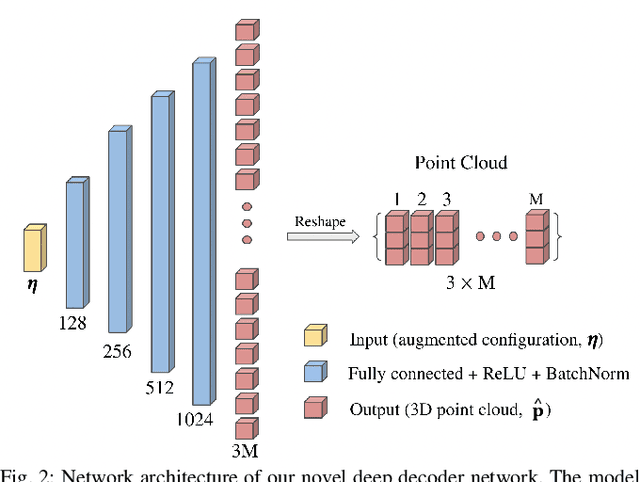
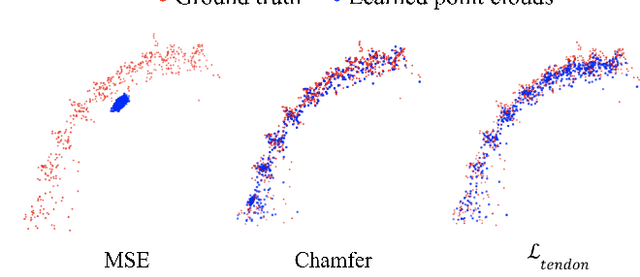
Tendon-driven continuum robots have been gaining popularity in medical applications due to their ability to curve around complex anatomical structures, potentially reducing the invasiveness of surgery. However, accurate modeling is required to plan and control the movements of these flexible robots. Physics-based models have limitations due to unmodeled effects, leading to mismatches between model prediction and actual robot shape. Recently proposed learning-based methods have been shown to overcome some of these limitations but do not account for hysteresis, a significant source of error for these robots. To overcome these challenges, we propose a novel deep decoder neural network that predicts the complete shape of tendon-driven robots using point clouds as the shape representation, conditioned on prior configurations to account for hysteresis. We evaluate our method on a physical tendon-driven robot and show that our network model accurately predicts the robot's shape, significantly outperforming a state-of-the-art physics-based model and a learning-based model that does not account for hysteresis.