Differentially Private Federated $k$-Means Clustering with Server-Side Data

Clustering is a cornerstone of data analysis that is particularly suited to identifying coherent subgroups or substructures in unlabeled data, as are generated continuously in large amounts these days. However, in many cases traditional clustering methods are not applicable, because data are increasingly being produced and stored in a distributed way, e.g. on edge devices, and privacy concerns prevent it from being transferred to a central server. To address this challenge, we present \acronym, a new algorithm for $k$-means clustering that is fully-federated as well as differentially private. Our approach leverages (potentially small and out-of-distribution) server-side data to overcome the primary challenge of differentially private clustering methods: the need for a good initialization. Combining our initialization with a simple federated DP-Lloyds algorithm we obtain an algorithm that achieves excellent results on synthetic and real-world benchmark tasks. We also provide a theoretical analysis of our method that provides bounds on the convergence speed and cluster identification success.

Federated Learning with Unlabeled Clients: Personalization Can Happen in Low Dimensions

Personalized federated learning has emerged as a popular approach to training on devices holding statistically heterogeneous data, known as clients. However, most existing approaches require a client to have labeled data for training or finetuning in order to obtain their own personalized model. In this paper we address this by proposing FLowDUP, a novel method that is able to generate a personalized model using only a forward pass with unlabeled data. The generated model parameters reside in a low-dimensional subspace, enabling efficient communication and computation. FLowDUP's learning objective is theoretically motivated by our new transductive multi-task PAC-Bayesian generalization bound, that provides performance guarantees for unlabeled clients. The objective is structured in such a way that it allows both clients with labeled data and clients with only unlabeled data to contribute to the training process. To supplement our theoretical results we carry out a thorough experimental evaluation of FLowDUP, demonstrating strong empirical performance on a range of datasets with differing sorts of statistically heterogeneous clients. Through numerous ablation studies, we test the efficacy of the individual components of the method.

Improved Modelling of Federated Datasets using Mixtures-of-Dirichlet-Multinomials

In practice, training using federated learning can be orders of magnitude slower than standard centralized training. This severely limits the amount of experimentation and tuning that can be done, making it challenging to obtain good performance on a given task. Server-side proxy data can be used to run training simulations, for instance for hyperparameter tuning. This can greatly speed up the training pipeline by reducing the number of tuning runs to be performed overall on the true clients. However, it is challenging to ensure that these simulations accurately reflect the dynamics of the real federated training. In particular, the proxy data used for simulations often comes as a single centralized dataset without a partition into distinct clients, and partitioning this data in a naive way can lead to simulations that poorly reflect real federated training. In this paper we address the challenge of how to partition centralized data in a way that reflects the statistical heterogeneity of the true federated clients. We propose a fully federated, theoretically justified, algorithm that efficiently learns the distribution of the true clients and observe improved server-side simulations when using the inferred distribution to create simulated clients from the centralized data.

PeFLL: A Lifelong Learning Approach to Personalized Federated Learning

Personalized federated learning (pFL) has emerged as a popular approach to dealing with the challenge of statistical heterogeneity between the data distributions of the participating clients. Instead of learning a single global model, pFL aims to learn an individual model for each client while still making use of the data available at other clients. In this work, we present PeFLL, a new pFL approach rooted in lifelong learning that performs well not only on clients present during its training phase, but also on any that may emerge in the future. PeFLL learns to output client specific models by jointly training an embedding network and a hypernetwork. The embedding network learns to represent clients in a latent descriptor space in a way that reflects their similarity to each other. The hypernetwork learns a mapping from this latent space to the space of possible client models. We demonstrate experimentally that PeFLL produces models of superior accuracy compared to previous methods, especially for clients not seen during training, and that it scales well to large numbers of clients. Moreover, generating a personalized model for a new client is efficient as no additional fine-tuning or optimization is required by either the client or the server. We also present theoretical results supporting PeFLL in the form of a new PAC-Bayesian generalization bound for lifelong learning and we prove the convergence of our proposed optimization procedure.

FedProp: Cross-client Label Propagation for Federated Semi-supervised Learning

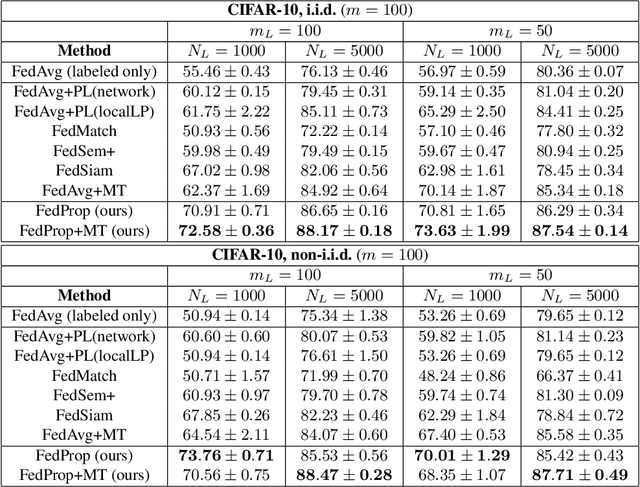
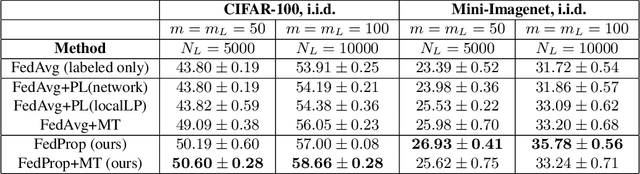
Federated learning (FL) allows multiple clients to jointly train a machine learning model in such a way that no client has to share their data with any other participating party. In the supervised setting, where all client data is fully labeled, FL has been widely adopted for learning tasks that require data privacy. However, it is an ongoing research question how to best perform federated learning in a semi-supervised setting, where the clients possess data that is only partially labeled or even completely unlabeled. In this work, we propose a new method, FedProp, that follows a manifold-based approach to semi-supervised learning (SSL). It estimates the data manifold jointly from the data of multiple clients and computes pseudo-labels using cross-client label propagation. To avoid that clients have to share their data with anyone, FedProp employs two cryptographically secure yet highly efficient protocols: secure Hamming distance computation and secure summation. Experiments on three standard benchmarks show that FedProp achieves higher classification accuracy than previous federated SSL methods. Furthermore, as a pseudolabel-based technique, FedProp is complementary to other federated SSL approaches, in particular consistency-based ones. We demonstrate experimentally that further accuracy gains are possible by combining both.