On the Theoretical Capacity of Evolution Strategies to Statistically Learn the Landscape Hessian

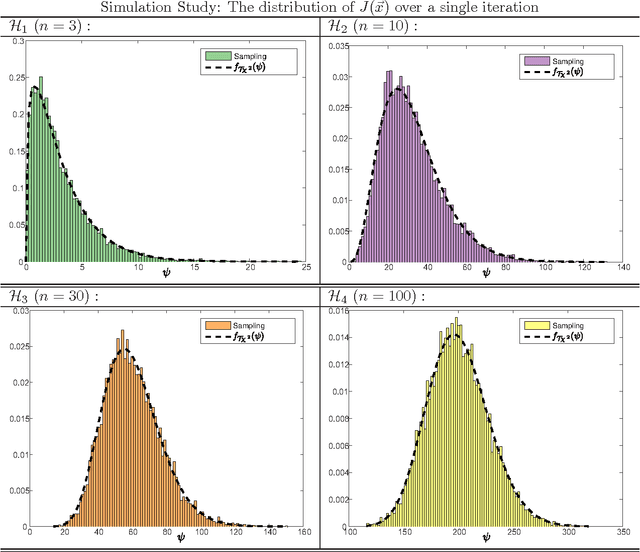
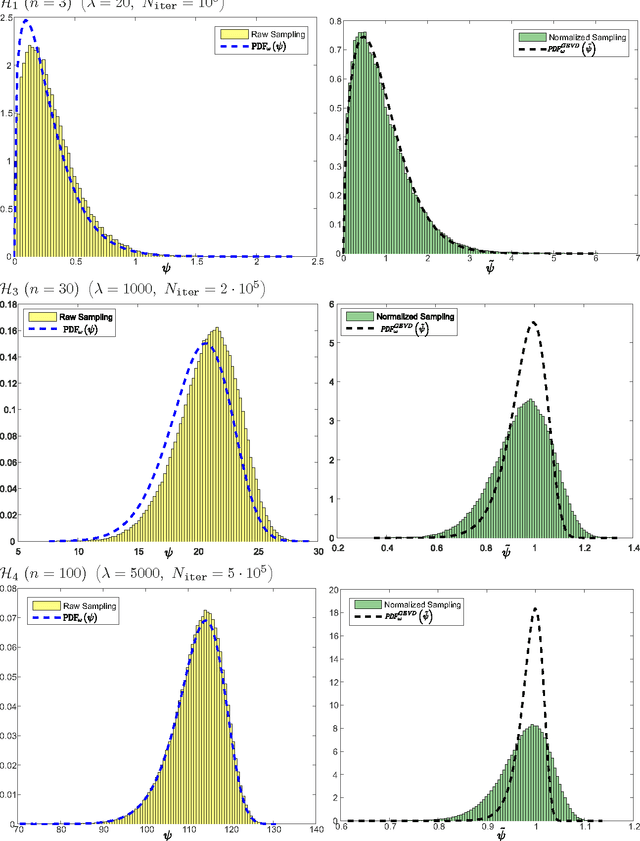
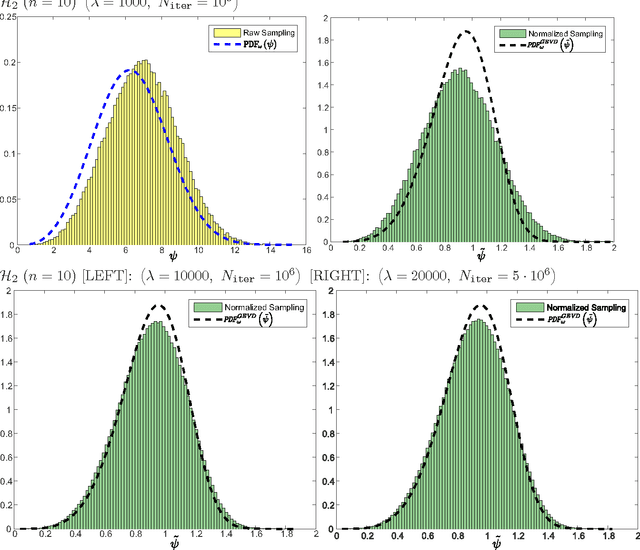
We study the theoretical capacity to statistically learn local landscape information by Evolution Strategies (ESs). Specifically, we investigate the covariance matrix when constructed by ESs operating with the selection operator alone. We model continuous generation of candidate solutions about quadratic basins of attraction, with deterministic selection of the decision vectors that minimize the objective function values. Our goal is to rigorously show that accumulation of winning individuals carries the potential to reveal valuable information about the search landscape, e.g., as already practically utilized by derandomized ES variants. We first show that the statistically-constructed covariance matrix over such winning decision vectors shares the same eigenvectors with the Hessian matrix about the optimum. We then provide an analytic approximation of this covariance matrix for a non-elitist multi-child $(1,\lambda)$-strategy, which holds for a large population size $\lambda$. Finally, we also numerically corroborate our results.

Quantum Control Experiments as a Testbed for Evolutionary Multi-Objective Algorithms

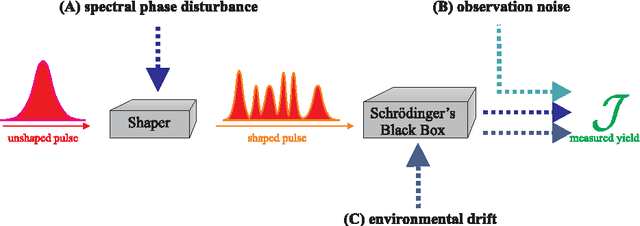
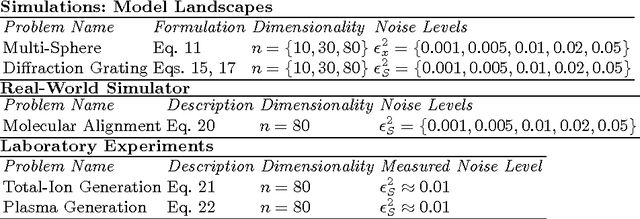
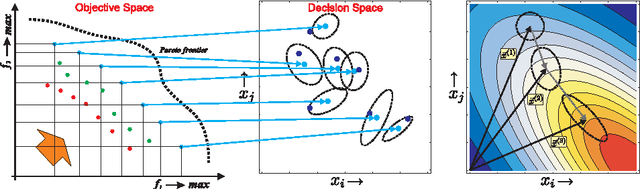
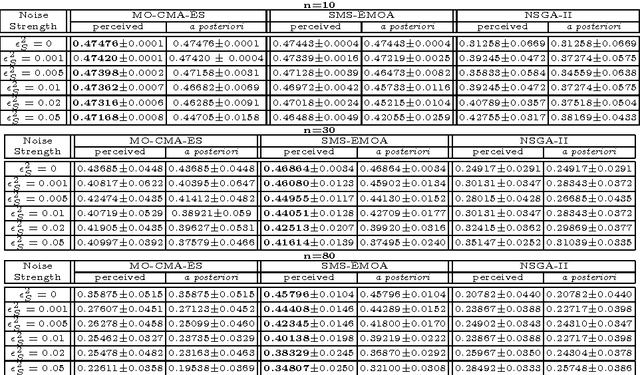
Experimental multi-objective Quantum Control is an emerging topic within the broad physics and chemistry applications domain of controlling quantum phenomena. This realm offers cutting edge ultrafast laser laboratory applications, which pose multiple objectives, noise, and possibly constraints on the high-dimensional search. In this study we introduce the topic of Multi-Observable Quantum Control (MOQC), and consider specific systems to be Pareto optimized subject to uncertainty, either experimentally or by means of simulated systems. The latter include a family of mathematical test-functions with a practical link to MOQC experiments, which are introduced here for the first time. We investigate the behavior of the multi-objective version of the Covariance Matrix Adaptation Evolution Strategy (MO-CMA-ES) and assess its performance on computer simulations as well as on laboratory closed-loop experiments. Overall, we propose a comprehensive study on experimental evolutionary Pareto optimization in high-dimensional continuous domains, draw some practical conclusions concerning the impact of fitness disturbance on algorithmic behavior, and raise several theoretical issues in the broad evolutionary multi-objective context.

Evolutionary Hessian Learning: Forced Optimal Covariance Adaptive Learning (FOCAL)

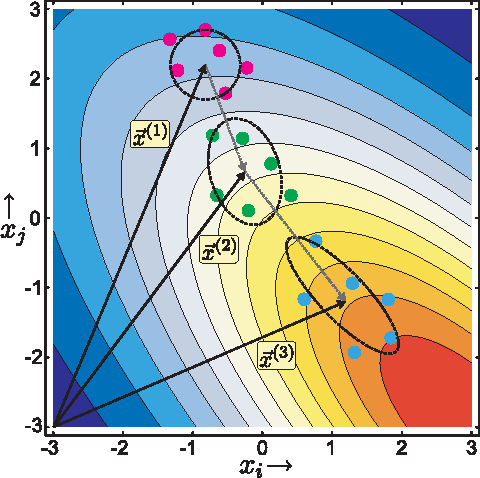
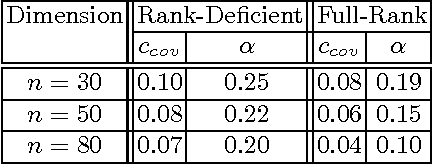
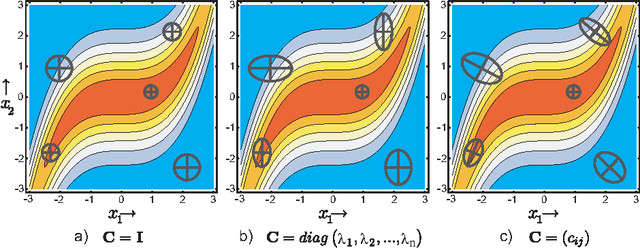
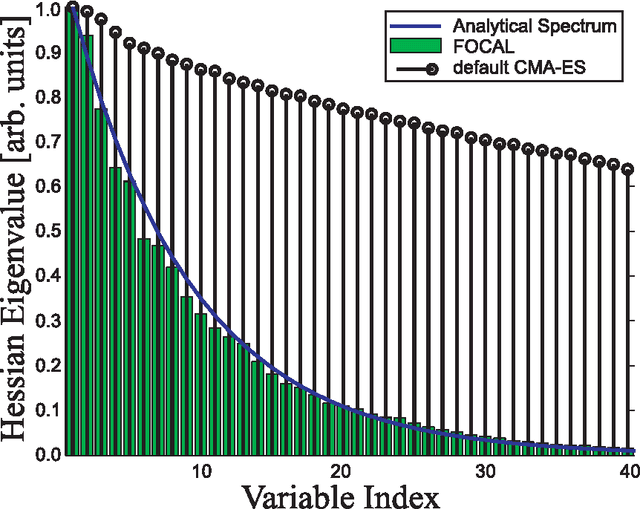
The Covariance Matrix Adaptation Evolution Strategy (CMA-ES) has been the most successful Evolution Strategy at exploiting covariance information; it uses a form of Principle Component Analysis which, under certain conditions, is suggested to converge to the correct covariance matrix, formulated as the inverse of the mathematically well-defined Hessian matrix. However, in practice, there exist conditions where CMA-ES converges to the global optimum (accomplishing its primary goal) while it does not learn the true covariance matrix (missing an auxiliary objective), likely due to step-size deficiency. These circumstances can involve high-dimensional landscapes with large condition numbers. This paper introduces a novel technique entitled Forced Optimal Covariance Adaptive Learning (FOCAL), with the explicit goal of determining the Hessian at the global basin of attraction. It begins by introducing theoretical foundations to the inverse relationship between the learned covariance and the Hessian matrices. FOCAL is then introduced and demonstrated to retrieve the Hessian matrix with high fidelity on both model landscapes and experimental Quantum Control systems, which are observed to possess a non-separable, non-quadratic search landscape. The recovered Hessian forms are corroborated by physical knowledge of the systems. This study constitutes an example for Natural Computing successfully serving other branches of natural sciences, and introducing at the same time a powerful generic method for any high-dimensional continuous search seeking landscape information.