On the Theoretical Capacity of Evolution Strategies to Statistically Learn the Landscape Hessian

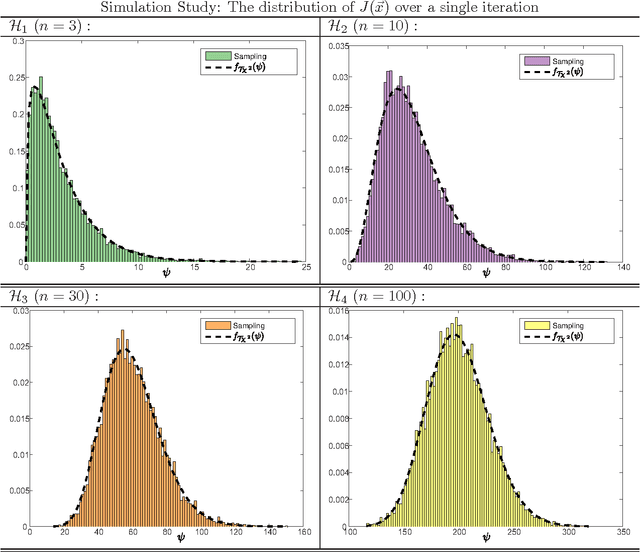
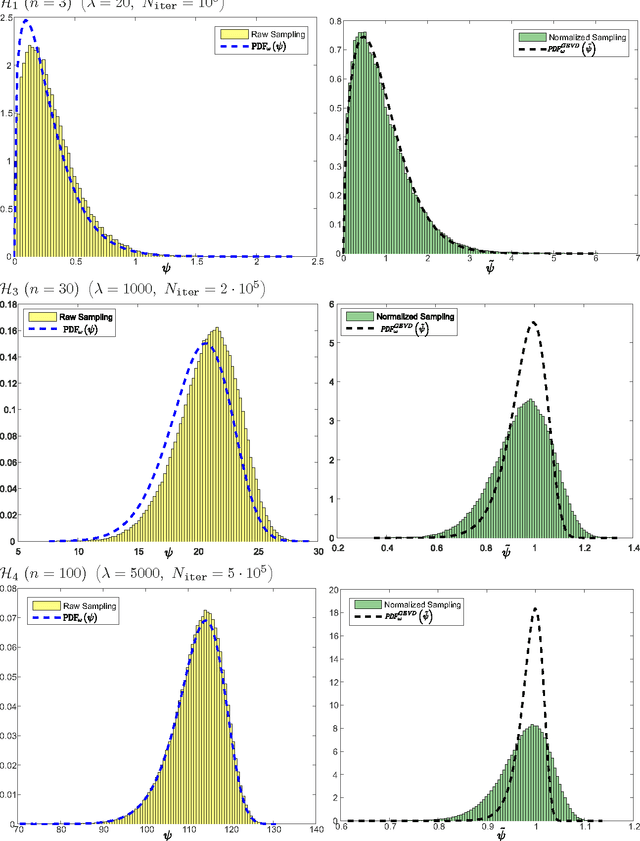
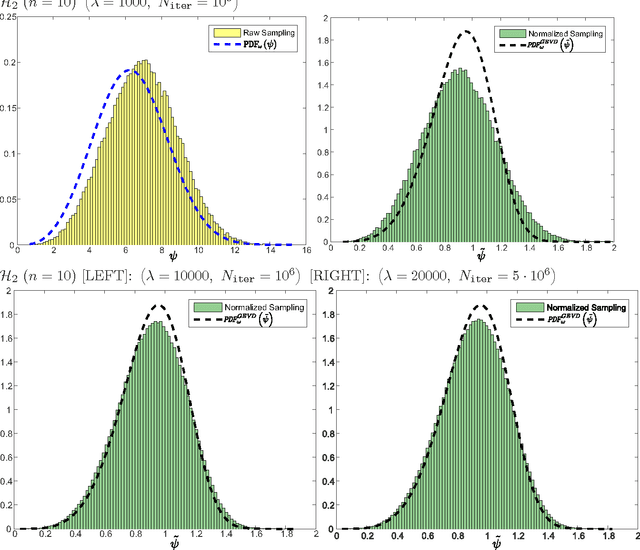
We study the theoretical capacity to statistically learn local landscape information by Evolution Strategies (ESs). Specifically, we investigate the covariance matrix when constructed by ESs operating with the selection operator alone. We model continuous generation of candidate solutions about quadratic basins of attraction, with deterministic selection of the decision vectors that minimize the objective function values. Our goal is to rigorously show that accumulation of winning individuals carries the potential to reveal valuable information about the search landscape, e.g., as already practically utilized by derandomized ES variants. We first show that the statistically-constructed covariance matrix over such winning decision vectors shares the same eigenvectors with the Hessian matrix about the optimum. We then provide an analytic approximation of this covariance matrix for a non-elitist multi-child $(1,\lambda)$-strategy, which holds for a large population size $\lambda$. Finally, we also numerically corroborate our results.