Attention-Based Transformer Networks for Quantum State Tomography

Neural networks have been actively explored for quantum state tomography (QST) due to their favorable expressibility. To further enhance the efficiency of reconstructing quantum states, we explore the similarity between language modeling and quantum state tomography and propose an attention-based QST method that utilizes the Transformer network to capture the correlations between measured results from different measurements. Our method directly retrieves the density matrices of quantum states from measured statistics, with the assistance of an integrated loss function that helps minimize the difference between the actual states and the retrieved states. Then, we systematically trace different impacts within a bag of common training strategies involving various parameter adjustments on the attention-based QST method. Combining these techniques, we establish a robust baseline that can efficiently reconstruct pure and mixed quantum states. Furthermore, by comparing the performance of three popular neural network architectures (FCNs, CNNs, and Transformer), we demonstrate the remarkable expressiveness of attention in learning density matrices from measured statistics.

Multi-Level Evolution Strategies for High-Resolution Black-Box Control

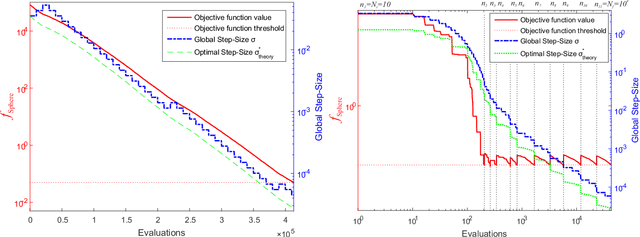
This paper introduces a multi-level (m-lev) mechanism into Evolution Strategies (ESs) in order to address a class of global optimization problems that could benefit from fine discretization of their decision variables. Such problems arise in engineering and scientific applications, which possess a multi-resolution control nature, and thus may be formulated either by means of low-resolution variants (providing coarser approximations with presumably lower accuracy for the general problem) or by high-resolution controls. A particular scientific application concerns practical Quantum Control (QC) problems, whose targeted optimal controls may be discretized to increasingly higher resolution, which in turn carries the potential to obtain better control yields. However, state-of-the-art derivative-free optimization heuristics for high-resolution formulations nominally call for an impractically large number of objective function calls. Therefore, an effective algorithmic treatment for such problems is needed. We introduce a framework with an automated scheme to facilitate guided-search over increasingly finer levels of control resolution for the optimization problem, whose on-the-fly learned parameters require careful adaptation. We instantiate the proposed m-lev self-adaptive ES framework by two specific strategies, namely the classical elitist single-child (1+1)-ES and the non-elitist multi-child derandomized $(\mu_W,\lambda)$-sep-CMA-ES. We first show that the approach is suitable by simulation-based optimization of QC systems which were heretofore viewed as too complex to address. We also present a laboratory proof-of-concept for the proposed approach on a basic experimental QC system objective.

Targeted Nonlinear Adversarial Perturbations in Images and Videos

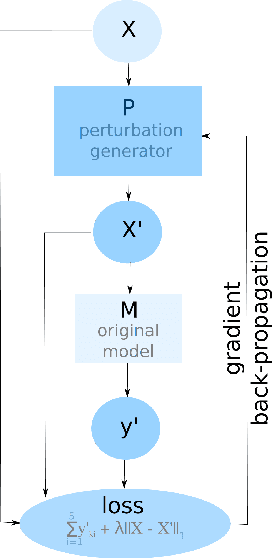
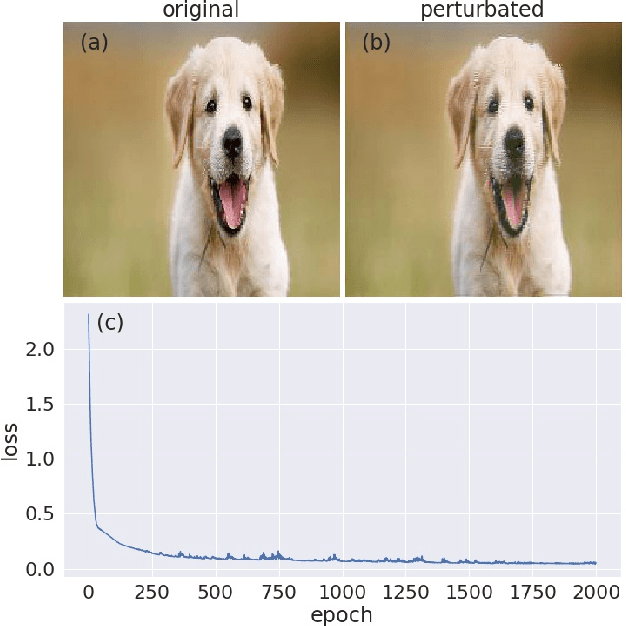
We introduce a method for learning adversarial perturbations targeted to individual images or videos. The learned perturbations are found to be sparse while at the same time containing a high level of feature detail. Thus, the extracted perturbations allow a form of object or action recognition and provide insights into what features the studied deep neural network models consider important when reaching their classification decisions. From an adversarial point of view, the sparse perturbations successfully confused the models into misclassifying, although the perturbed samples still belonged to the same original class by visual examination. This is discussed in terms of a prospective data augmentation scheme. The sparse yet high-quality perturbations may also be leveraged for image or video compression.

High Dimensional Model Representation as a Glass Box in Supervised Machine Learning

Prediction and explanation are key objects in supervised machine learning, where predictive models are known as black boxes and explanatory models are known as glass boxes. Explanation provides the necessary and sufficient information to interpret the model output in terms of the model input. It includes assessments of model output dependence on important input variables and measures of input variable importance to model output. High dimensional model representation (HDMR), also known as the generalized functional ANOVA expansion, provides useful insight into the input-output behavior of supervised machine learning models. This article gives applications of HDMR in supervised machine learning. The first application is characterizing information leakage in ``big-data'' settings. The second application is reduced-order representation of elementary symmetric polynomials. The third application is analysis of variance with correlated variables. The last application is estimation of HDMR from kernel machine and decision tree black box representations. These results suggest HDMR to have broad utility within machine learning as a glass box representation.

Differential Evolution for Quantum Robust Control: Algorithm, Applications and Experiments

Robust control design for quantum systems has been recognized as a key task in quantum information technology, molecular chemistry and atomic physics. In this paper, an improved differential evolution algorithm of msMS_DE is proposed to search robust fields for various quantum control problems. In msMS_DE, multiple samples are used for fitness evaluation and a mixed strategy is employed for mutation operation. In particular, the msMS_DE algorithm is applied to the control problem of open inhomogeneous quantum ensembles and the consensus problem of a quantum network with uncertainties. Numerical results are presented to demonstrate the excellent performance of the improved DE algorithm for these two classes of quantum robust control problems. Furthermore, msMS_DE is experimentally implemented on femtosecond laser control systems to generate good signals of two photon absorption and control fragmentation of halomethane molecules CH2BrI. Experimental results demonstrate excellent performance of msMS_DE in searching effective femtosecond laser pulses for various tasks.

Quantum Control Experiments as a Testbed for Evolutionary Multi-Objective Algorithms

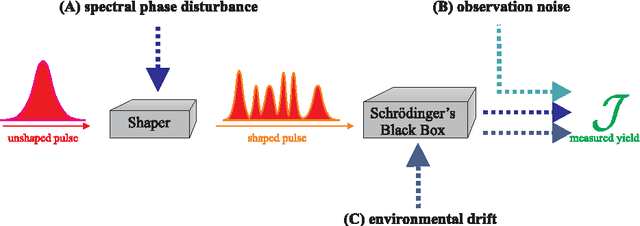
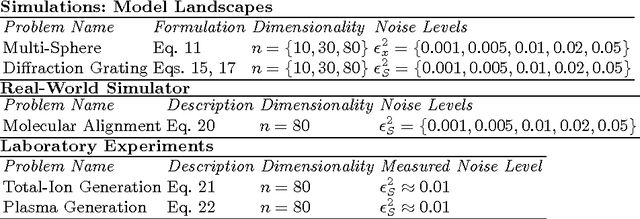
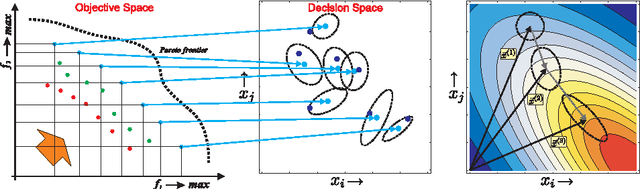
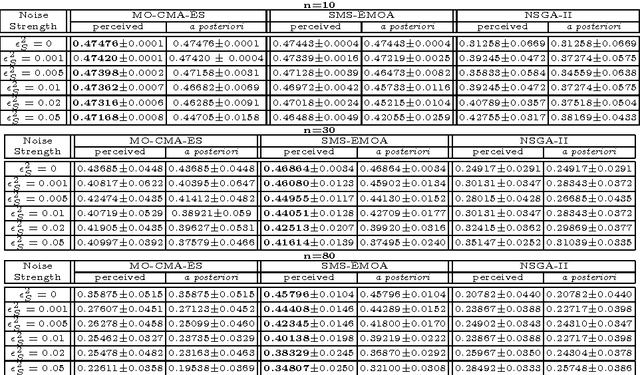
Experimental multi-objective Quantum Control is an emerging topic within the broad physics and chemistry applications domain of controlling quantum phenomena. This realm offers cutting edge ultrafast laser laboratory applications, which pose multiple objectives, noise, and possibly constraints on the high-dimensional search. In this study we introduce the topic of Multi-Observable Quantum Control (MOQC), and consider specific systems to be Pareto optimized subject to uncertainty, either experimentally or by means of simulated systems. The latter include a family of mathematical test-functions with a practical link to MOQC experiments, which are introduced here for the first time. We investigate the behavior of the multi-objective version of the Covariance Matrix Adaptation Evolution Strategy (MO-CMA-ES) and assess its performance on computer simulations as well as on laboratory closed-loop experiments. Overall, we propose a comprehensive study on experimental evolutionary Pareto optimization in high-dimensional continuous domains, draw some practical conclusions concerning the impact of fitness disturbance on algorithmic behavior, and raise several theoretical issues in the broad evolutionary multi-objective context.

Evolutionary Hessian Learning: Forced Optimal Covariance Adaptive Learning (FOCAL)

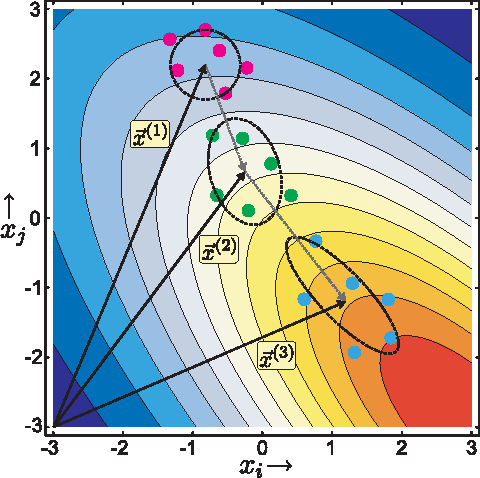
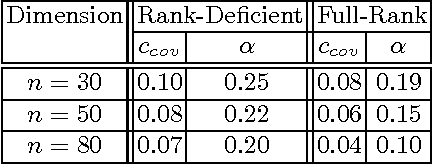
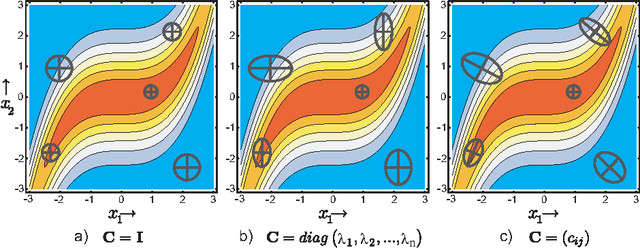
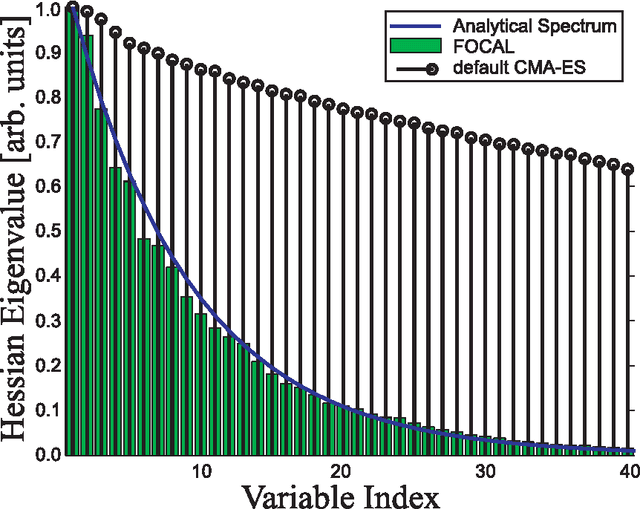
The Covariance Matrix Adaptation Evolution Strategy (CMA-ES) has been the most successful Evolution Strategy at exploiting covariance information; it uses a form of Principle Component Analysis which, under certain conditions, is suggested to converge to the correct covariance matrix, formulated as the inverse of the mathematically well-defined Hessian matrix. However, in practice, there exist conditions where CMA-ES converges to the global optimum (accomplishing its primary goal) while it does not learn the true covariance matrix (missing an auxiliary objective), likely due to step-size deficiency. These circumstances can involve high-dimensional landscapes with large condition numbers. This paper introduces a novel technique entitled Forced Optimal Covariance Adaptive Learning (FOCAL), with the explicit goal of determining the Hessian at the global basin of attraction. It begins by introducing theoretical foundations to the inverse relationship between the learned covariance and the Hessian matrices. FOCAL is then introduced and demonstrated to retrieve the Hessian matrix with high fidelity on both model landscapes and experimental Quantum Control systems, which are observed to possess a non-separable, non-quadratic search landscape. The recovered Hessian forms are corroborated by physical knowledge of the systems. This study constitutes an example for Natural Computing successfully serving other branches of natural sciences, and introducing at the same time a powerful generic method for any high-dimensional continuous search seeking landscape information.