On convex conceptual regions in deep network representations

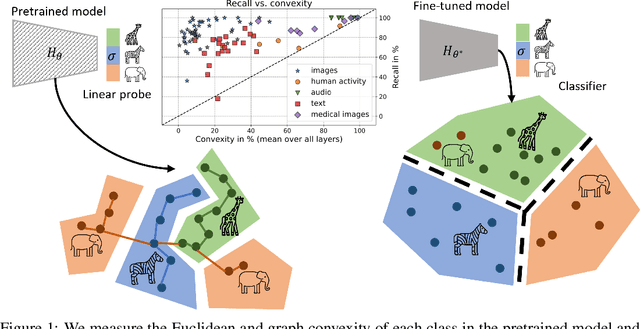
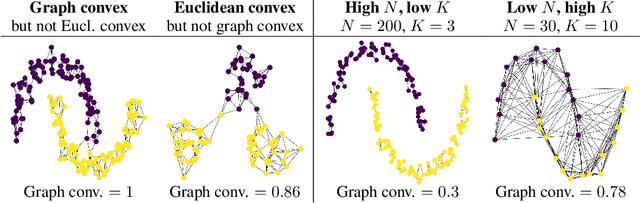
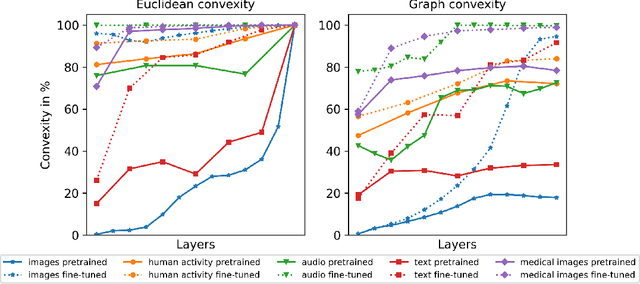
The current study of human-machine alignment aims at understanding the geometry of latent spaces and the correspondence to human representations. G\"ardenfors' conceptual spaces is a prominent framework for understanding human representations. Convexity of object regions in conceptual spaces is argued to promote generalizability, few-shot learning, and intersubject alignment. Based on these insights, we investigate the notion of convexity of concept regions in machine-learned latent spaces. We develop a set of tools for measuring convexity in sampled data and evaluate emergent convexity in layered representations of state-of-the-art deep networks. We show that convexity is robust to basic re-parametrization, hence, meaningful as a quality of machine-learned latent spaces. We find that approximate convexity is pervasive in neural representations in multiple application domains, including models of images, audio, human activity, text, and brain data. We measure convexity separately for labels (i.e., targets for fine-tuning) and other concepts. Generally, we observe that fine-tuning increases the convexity of label regions, while for more general concepts, it depends on the alignment of the concept with the fine-tuning objective. We find evidence that pre-training convexity of class label regions predicts subsequent fine-tuning performance.

On the role of Model Uncertainties in Bayesian Optimization

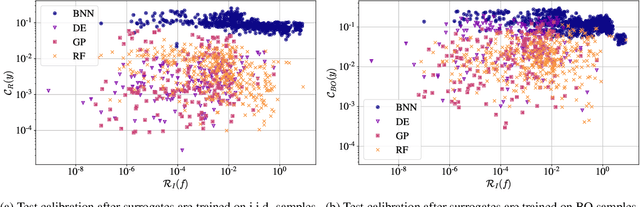
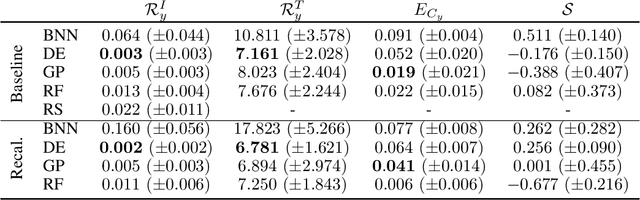
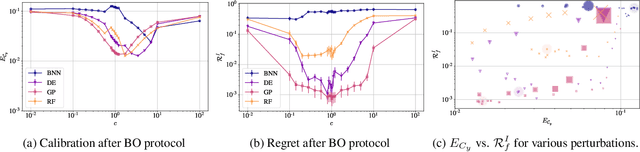
Bayesian optimization (BO) is a popular method for black-box optimization, which relies on uncertainty as part of its decision-making process when deciding which experiment to perform next. However, not much work has addressed the effect of uncertainty on the performance of the BO algorithm and to what extent calibrated uncertainties improve the ability to find the global optimum. In this work, we provide an extensive study of the relationship between the BO performance (regret) and uncertainty calibration for popular surrogate models and compare them across both synthetic and real-world experiments. Our results confirm that Gaussian Processes are strong surrogate models and that they tend to outperform other popular models. Our results further show a positive association between calibration error and regret, but interestingly, this association disappears when we control for the type of model in the analysis. We also studied the effect of re-calibration and demonstrate that it generally does not lead to improved regret. Finally, we provide theoretical justification for why uncertainty calibration might be difficult to combine with BO due to the small sample sizes commonly used.