Evaluation of radiomic feature harmonization techniques for benign and malignant pulmonary nodules

BACKGROUND: Radiomics provides quantitative features of pulmonary nodules (PNs) which could aid lung cancer diagnosis, but medical image acquisition variability is an obstacle to clinical application. Acquisition effects may differ between radiomic features from benign vs. malignant PNs. PURPOSE: We evaluated how to account for differences between benign and malignant PNs when correcting radiomic features' acquisition dependency. METHODS: We used 567 chest CT scans grouped as benign, malignant, or lung cancer screening (mixed benign, malignant). ComBat harmonization was applied to extracted features for variation in 4 acquisition parameters. We compared: harmonizing without distinction, harmonizing with a covariate to preserve distinctions between subgroups, and harmonizing subgroups separately. Significant ($p\le0.05$) Kruskal-Wallis tests showed whether harmonization removed acquisition dependency. A LASSO-SVM pipeline was trained on successfully harmonized features to predict malignancy. To evaluate predictive information in these features, the trained harmonization estimators and predictive model were applied to unseen test sets. Harmonization and predictive performance were assessed for 10 trials of 5-fold cross-validation. RESULTS: An average 2.1% of features (95% CI:1.9-2.4%) were acquisition-independent when harmonized without distinction, 27.3% (95% CI:25.7-28.9%) when harmonized with a covariate, and 90.9% (95% CI:90.4-91.5%) when harmonized separately. Data harmonized separately or with a covariate trained models with higher ROC-AUC for screening scans than data harmonized without distinction between benign and malignant PNs (Delong test, adjusted $p\le0.05$). CONCLUSIONS: Radiomic features of benign and malignant PNs need different corrective transformations to recover acquisition-independent distributions. This can be done by harmonizing separately or with a covariate.

Harnessing the Power of Gradient-Based Simulations for Multi-Objective Optimization in Particle Accelerators

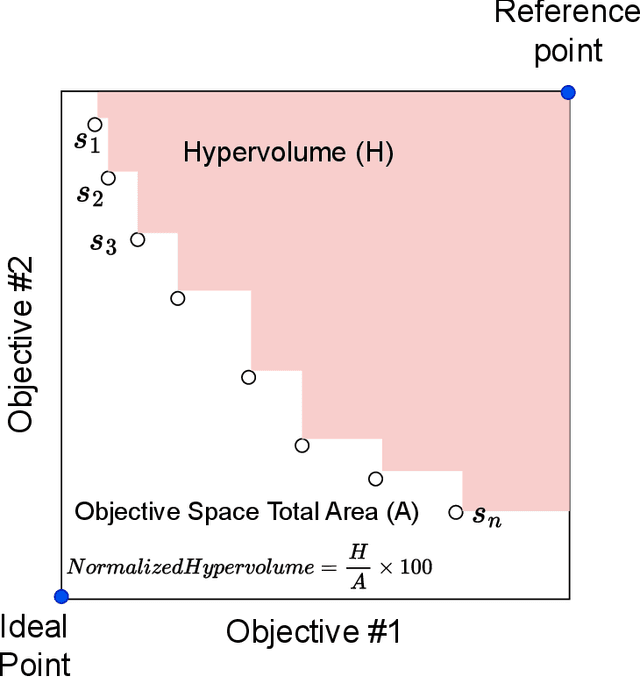
Particle accelerator operation requires simultaneous optimization of multiple objectives. Multi-Objective Optimization (MOO) is particularly challenging due to trade-offs between the objectives. Evolutionary algorithms, such as genetic algorithm (GA), have been leveraged for many optimization problems, however, they do not apply to complex control problems by design. This paper demonstrates the power of differentiability for solving MOO problems using a Deep Differentiable Reinforcement Learning (DDRL) algorithm in particle accelerators. We compare DDRL algorithm with Model Free Reinforcement Learning (MFRL), GA and Bayesian Optimization (BO) for simultaneous optimization of heat load and trip rates in the Continuous Electron Beam Accelerator Facility (CEBAF). The underlying problem enforces strict constraints on both individual states and actions as well as cumulative (global) constraint for energy requirements of the beam. A physics-based surrogate model based on real data is developed. This surrogate model is differentiable and allows back-propagation of gradients. The results are evaluated in the form of a Pareto-front for two objectives. We show that the DDRL outperforms MFRL, BO, and GA on high dimensional problems.

Zyxin is all you need: machine learning adherent cell mechanics

Cellular form and function emerge from complex mechanochemical systems within the cytoplasm. No systematic strategy currently exists to infer large-scale physical properties of a cell from its many molecular components. This is a significant obstacle to understanding biophysical processes such as cell adhesion and migration. Here, we develop a data-driven biophysical modeling approach to learn the mechanical behavior of adherent cells. We first train neural networks to predict forces generated by adherent cells from images of cytoskeletal proteins. Strikingly, experimental images of a single focal adhesion protein, such as zyxin, are sufficient to predict forces and generalize to unseen biological regimes. This protein field alone contains enough information to yield accurate predictions even if forces themselves are generated by many interacting proteins. We next develop two approaches - one explicitly constrained by physics, the other more agnostic - that help construct data-driven continuum models of cellular forces using this single focal adhesion field. Both strategies consistently reveal that cellular forces are encoded by two different length scales in adhesion protein distributions. Beyond adherent cell mechanics, our work serves as a case study for how to integrate neural networks in the construction of predictive phenomenological models in cell biology, even when little knowledge of the underlying microscopic mechanisms exist.