Towards General Neural Surrogate Solvers with Specialized Neural Accelerators

Surrogate neural network-based partial differential equation (PDE) solvers have the potential to solve PDEs in an accelerated manner, but they are largely limited to systems featuring fixed domain sizes, geometric layouts, and boundary conditions. We propose Specialized Neural Accelerator-Powered Domain Decomposition Methods (SNAP-DDM), a DDM-based approach to PDE solving in which subdomain problems containing arbitrary boundary conditions and geometric parameters are accurately solved using an ensemble of specialized neural operators. We tailor SNAP-DDM to 2D electromagnetics and fluidic flow problems and show how innovations in network architecture and loss function engineering can produce specialized surrogate subdomain solvers with near unity accuracy. We utilize these solvers with standard DDM algorithms to accurately solve freeform electromagnetics and fluids problems featuring a wide range of domain sizes.

Large-scale global optimization of ultra-high dimensional non-convex landscapes based on generative neural networks

We present a non-convex optimization algorithm metaheuristic, based on the training of a deep generative network, which enables effective searching within continuous, ultra-high dimensional landscapes. During network training, populations of sampled local gradients are utilized within a customized loss function to evolve the network output distribution function towards one peak at high-performing optima. The deep network architecture is tailored to support progressive growth over the course of training, which allows the algorithm to manage the curse of dimensionality characteristic of high-dimensional landscapes. We apply our concept to a range of standard optimization problems with dimensions as high as one thousand and show that our method performs better with fewer function evaluations compared to state-of-the-art algorithm benchmarks. We also discuss the role of deep network over-parameterization, loss function engineering, and proper network architecture selection in optimization, and why the required batch size of sampled local gradients is independent of problem dimension. These concepts form the foundation for a new class of algorithms that utilize customizable and expressive deep generative networks to solve non-convex optimization problems.

WaveY-Net: Physics-augmented deep learning for high-speed electromagnetic simulation and optimization

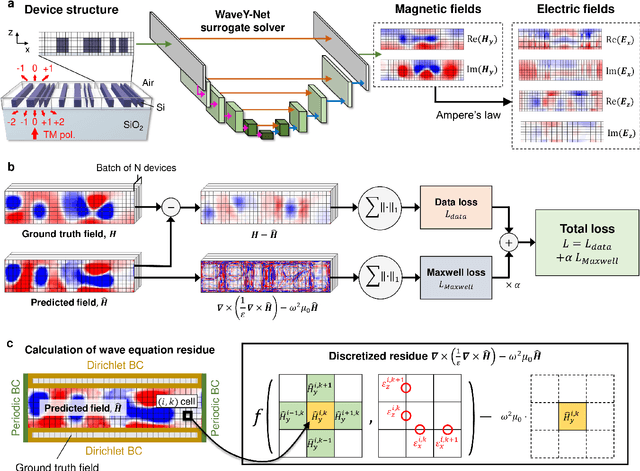
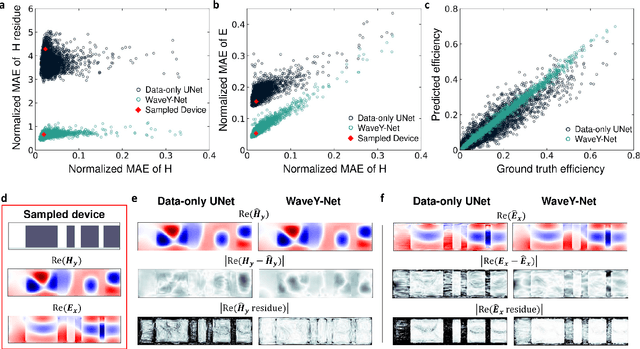
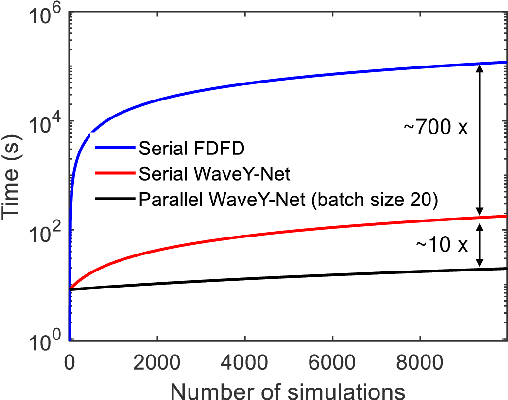
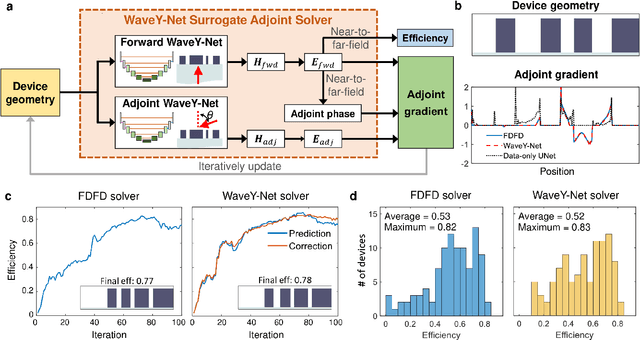
The calculation of electromagnetic field distributions within structured media is central to the optimization and validation of photonic devices. We introduce WaveY-Net, a hybrid data- and physics-augmented convolutional neural network that can predict electromagnetic field distributions with ultra fast speeds and high accuracy for entire classes of dielectric photonic structures. This accuracy is achieved by training the neural network to learn only the magnetic near-field distributions of a system and to use a discrete formalism of Maxwell's equations in two ways: as physical constraints in the loss function and as a means to calculate the electric fields from the magnetic fields. As a model system, we construct a surrogate simulator for periodic silicon nanostructure arrays and show that the high speed simulator can be directly and effectively used in the local and global freeform optimization of metagratings. We anticipate that physics-augmented networks will serve as a viable Maxwell simulator replacement for many classes of photonic systems, transforming the way they are designed.

Multi-objective and categorical global optimization of photonic structures based on ResNet generative neural networks

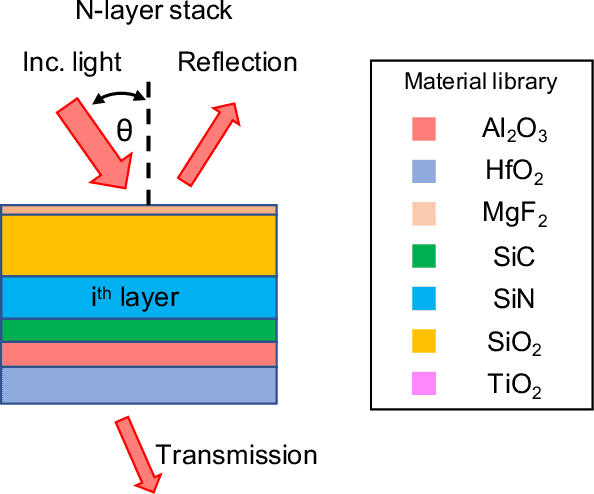
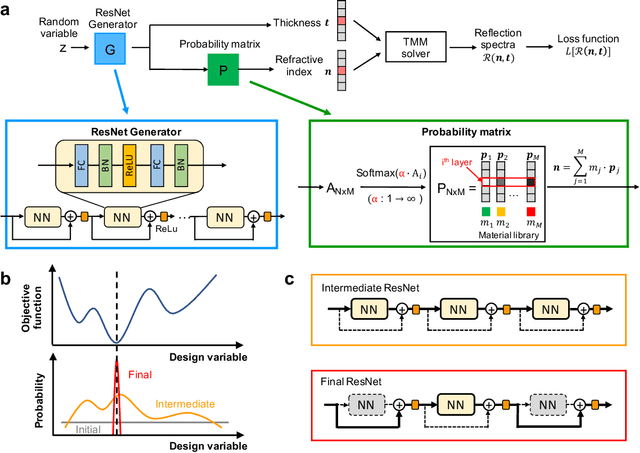
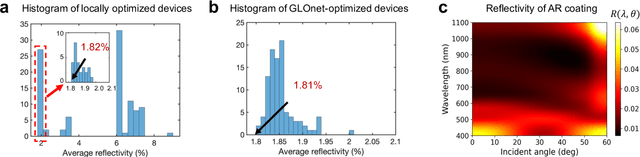
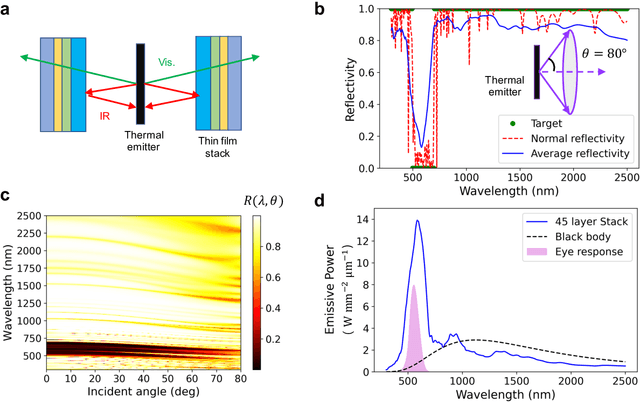
We show that deep generative neural networks, based on global topology optimization networks (GLOnets), can be configured to perform the multi-objective and categorical global optimization of photonic devices. A residual network scheme enables GLOnets to evolve from a deep architecture, which is required to properly search the full design space early in the optimization process, to a shallow network that generates a narrow distribution of globally optimal devices. As a proof-of-concept demonstration, we adapt our method to design thin film stacks consisting of multiple material types. Benchmarks with known globally-optimized anti-reflection structures indicate that GLOnets can find the global optimum with orders of magnitude faster speeds compared to conventional algorithms. We also demonstrate the utility of our method in complex design tasks with its application to incandescent light filters. These results indicate that advanced concepts in deep learning can push the capabilities of inverse design algorithms for photonics.

Deep neural networks for the evaluation and design of photonic devices

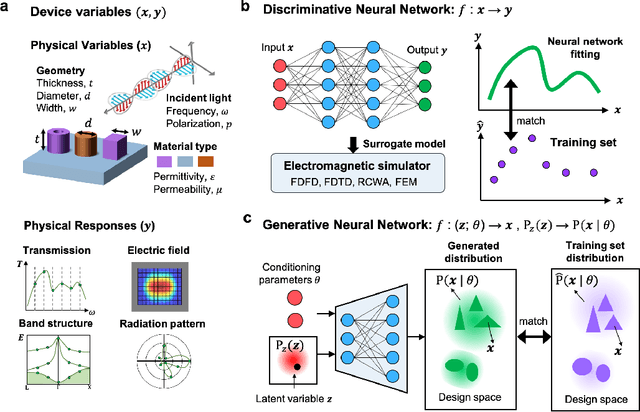
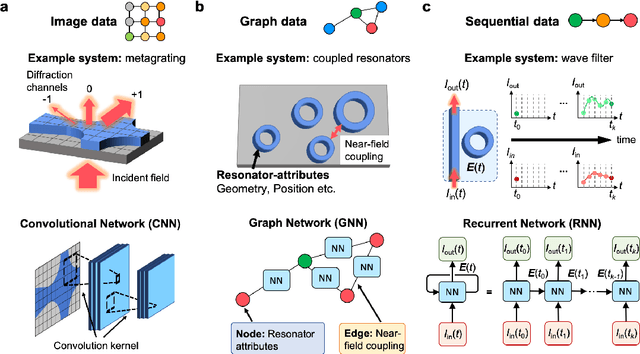
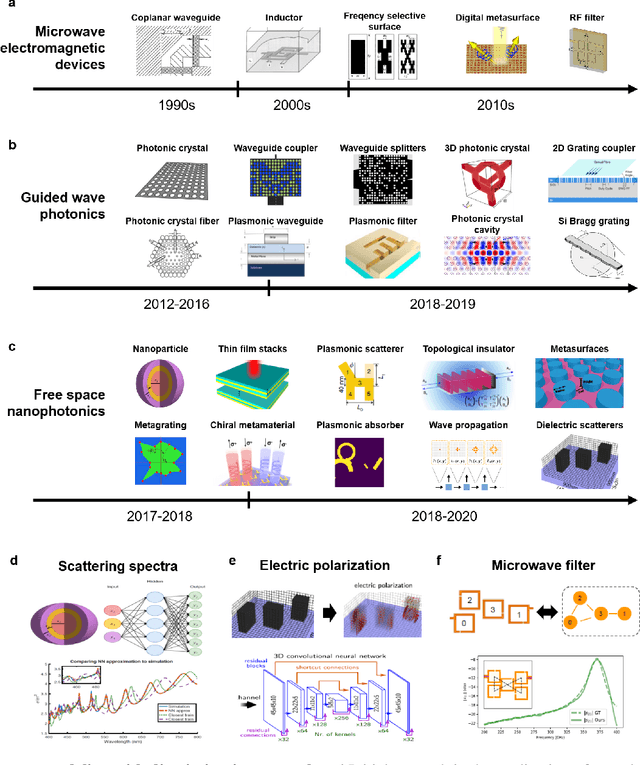
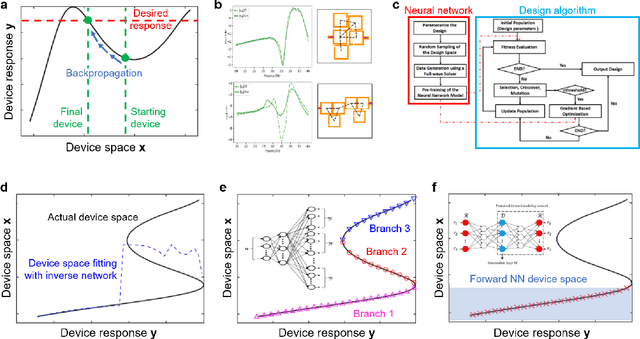
The data sciences revolution is poised to transform the way photonic systems are simulated and designed. Photonics are in many ways an ideal substrate for machine learning: the objective of much of computational electromagnetics is the capture of non-linear relationships in high dimensional spaces, which is the core strength of neural networks. Additionally, the mainstream availability of Maxwell solvers makes the training and evaluation of neural networks broadly accessible and tailorable to specific problems. In this Review, we will show how deep neural networks, configured as discriminative networks, can learn from training sets and operate as high-speed surrogate electromagnetic solvers. We will also examine how deep generative networks can learn geometric features in device distributions and even be configured to serve as robust global optimizers. Fundamental data sciences concepts framed within the context of photonics will also be discussed, including the network training process, delineation of different network classes and architectures, and dimensionality reduction.

Progressive-Growing of Generative Adversarial Networks for Metasurface Optimization

Generative adversarial networks, which can generate metasurfaces based on a training set of high performance device layouts, have the potential to significantly reduce the computational cost of the metasurface design process. However, basic GAN architectures are unable to fully capture the detailed features of topologically complex metasurfaces, and generated devices therefore require additional computationally-expensive design refinement. In this Letter, we show that GANs can better learn spatially fine features from high-resolution training data by progressively growing its network architecture and training set. Our results indicate that with this training methodology, the best generated devices have performances that compare well with the best devices produced by gradient-based topology optimization, thereby eliminating the need for additional design refinement. We envision that this network training method can generalize to other physical systems where device performance is strongly correlated with fine geometric structuring.

Dataless training of generative models for the inverse design of metasurfaces

Metasurfaces are subwavelength-structured artificial media that can shape and localize electromagnetic waves in unique ways. The inverse design of metasurfaces is a non-convex optimization problem in a high dimensional space, making global optimization a huge challenge. We present a new type of global optimization algorithm, based on the training of a generative neural network without a training set, which can produce high-performance metasurfaces. Instead of directly optimizing devices one at a time, we reframe the optimization as the training of a generator that iteratively enhances the probability of generating high-performance devices. The loss function used for backpropagation is defined as a function of generated patterns and their efficiency gradients, which are calculated by the adjoint variable method using the forward and adjoint electromagnetic simulations. We observe that distributions of devices generated by the network continuously shift towards high-performance design space regions over the course of optimization. Upon training completion, the best-generated devices have efficiencies comparable to or exceeding the best devices designed using standard topology optimization. We envision that our proposed global optimization algorithm generally applies to other gradient-based optimization problems in optics, mechanics and electronics.

Data-driven metasurface discovery

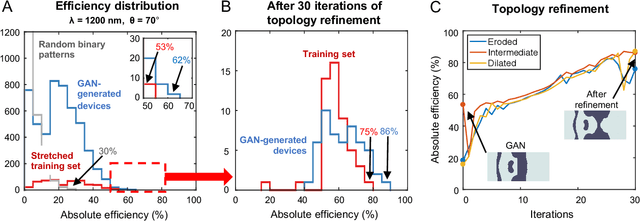
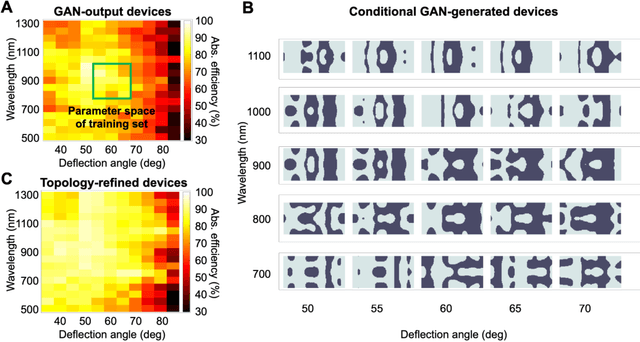
A long-standing challenge with metasurface design is identifying computationally efficient methods that produce high performance devices. Design methods based on iterative optimization push the performance limits of metasurfaces, but they require extensive computational resources that limit their implementation to small numbers of microscale devices. We show that generative neural networks can learn from a small set of topology-optimized metasurfaces to produce large numbers of high-efficiency, topologically-complex metasurfaces operating across a large parameter space. This approach enables considerable savings in computation cost compared to brute force optimization. As a model system, we employ conditional generative adversarial networks to design highly-efficient metagratings over a broad range of deflection angles and operating wavelengths. Generated device designs can be further locally optimized and serve as additional training data for network refinement. Our design concept utilizes a relatively small initial training set of just a few hundred devices, and it serves as a more general blueprint for the AI-based analysis of physical systems where access to large datasets is limited. We envision that such data-driven design tools can be broadly utilized in other domains of optics, acoustics, mechanics, and electronics.