Dataless training of generative models for the inverse design of metasurfaces

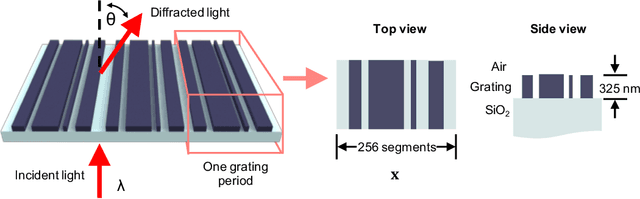
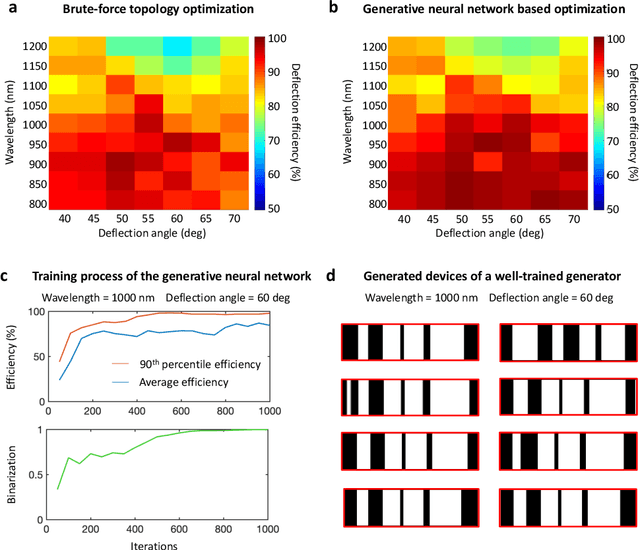
Metasurfaces are subwavelength-structured artificial media that can shape and localize electromagnetic waves in unique ways. The inverse design of metasurfaces is a non-convex optimization problem in a high dimensional space, making global optimization a huge challenge. We present a new type of global optimization algorithm, based on the training of a generative neural network without a training set, which can produce high-performance metasurfaces. Instead of directly optimizing devices one at a time, we reframe the optimization as the training of a generator that iteratively enhances the probability of generating high-performance devices. The loss function used for backpropagation is defined as a function of generated patterns and their efficiency gradients, which are calculated by the adjoint variable method using the forward and adjoint electromagnetic simulations. We observe that distributions of devices generated by the network continuously shift towards high-performance design space regions over the course of optimization. Upon training completion, the best-generated devices have efficiencies comparable to or exceeding the best devices designed using standard topology optimization. We envision that our proposed global optimization algorithm generally applies to other gradient-based optimization problems in optics, mechanics and electronics.