Towards General Neural Surrogate Solvers with Specialized Neural Accelerators

Surrogate neural network-based partial differential equation (PDE) solvers have the potential to solve PDEs in an accelerated manner, but they are largely limited to systems featuring fixed domain sizes, geometric layouts, and boundary conditions. We propose Specialized Neural Accelerator-Powered Domain Decomposition Methods (SNAP-DDM), a DDM-based approach to PDE solving in which subdomain problems containing arbitrary boundary conditions and geometric parameters are accurately solved using an ensemble of specialized neural operators. We tailor SNAP-DDM to 2D electromagnetics and fluidic flow problems and show how innovations in network architecture and loss function engineering can produce specialized surrogate subdomain solvers with near unity accuracy. We utilize these solvers with standard DDM algorithms to accurately solve freeform electromagnetics and fluids problems featuring a wide range of domain sizes.

WaveY-Net: Physics-augmented deep learning for high-speed electromagnetic simulation and optimization

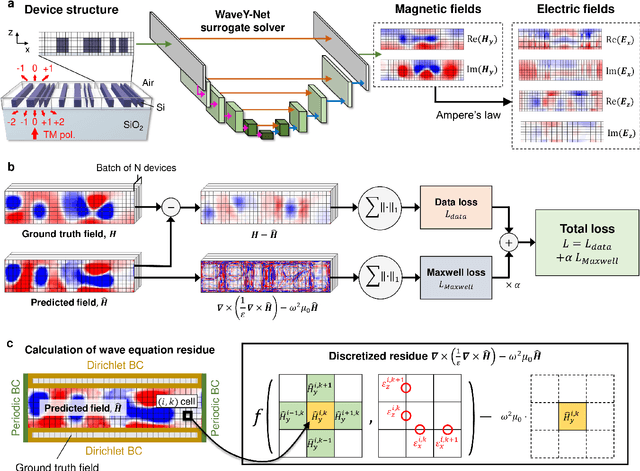
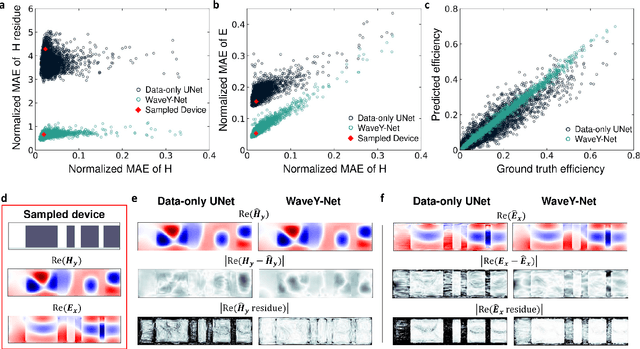
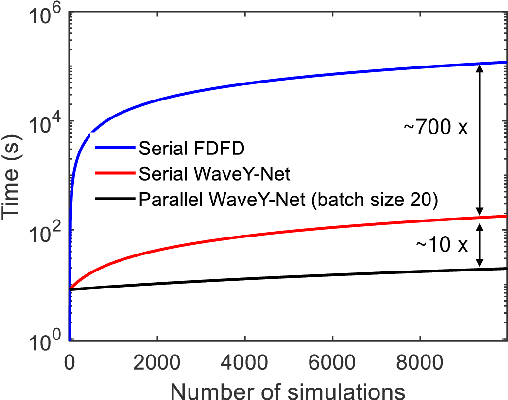
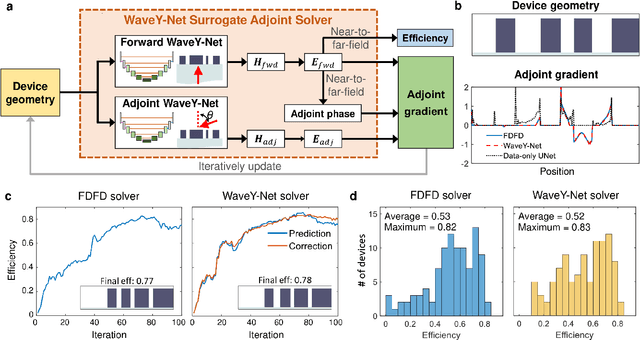
The calculation of electromagnetic field distributions within structured media is central to the optimization and validation of photonic devices. We introduce WaveY-Net, a hybrid data- and physics-augmented convolutional neural network that can predict electromagnetic field distributions with ultra fast speeds and high accuracy for entire classes of dielectric photonic structures. This accuracy is achieved by training the neural network to learn only the magnetic near-field distributions of a system and to use a discrete formalism of Maxwell's equations in two ways: as physical constraints in the loss function and as a means to calculate the electric fields from the magnetic fields. As a model system, we construct a surrogate simulator for periodic silicon nanostructure arrays and show that the high speed simulator can be directly and effectively used in the local and global freeform optimization of metagratings. We anticipate that physics-augmented networks will serve as a viable Maxwell simulator replacement for many classes of photonic systems, transforming the way they are designed.

Deep neural networks for the evaluation and design of photonic devices

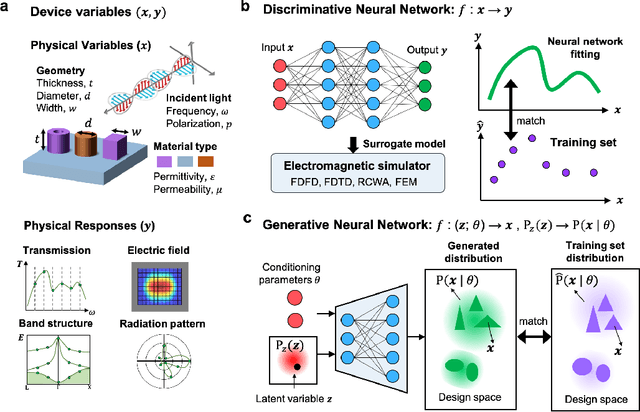
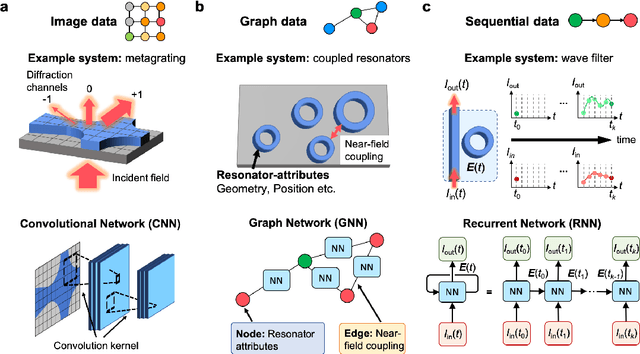
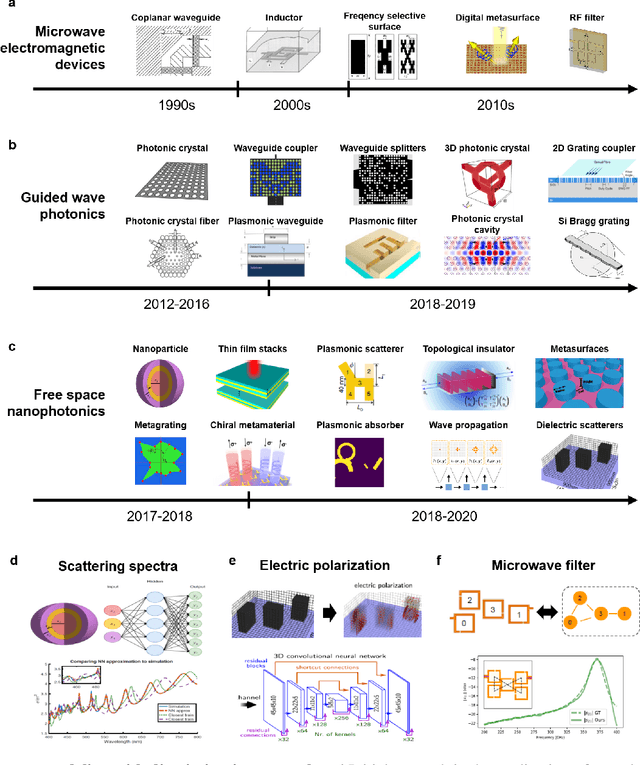
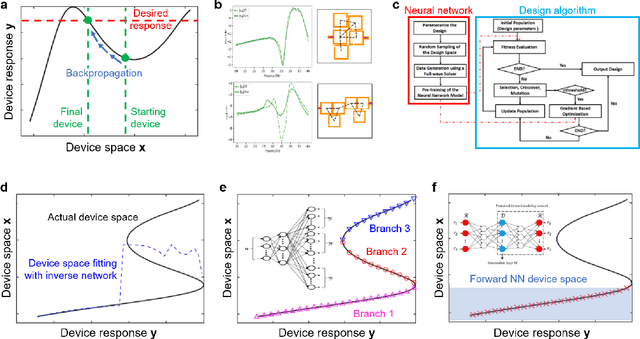
The data sciences revolution is poised to transform the way photonic systems are simulated and designed. Photonics are in many ways an ideal substrate for machine learning: the objective of much of computational electromagnetics is the capture of non-linear relationships in high dimensional spaces, which is the core strength of neural networks. Additionally, the mainstream availability of Maxwell solvers makes the training and evaluation of neural networks broadly accessible and tailorable to specific problems. In this Review, we will show how deep neural networks, configured as discriminative networks, can learn from training sets and operate as high-speed surrogate electromagnetic solvers. We will also examine how deep generative networks can learn geometric features in device distributions and even be configured to serve as robust global optimizers. Fundamental data sciences concepts framed within the context of photonics will also be discussed, including the network training process, delineation of different network classes and architectures, and dimensionality reduction.