John Y. Shin
Compressing Heavy-Tailed Weight Matrices for Non-Vacuous Generalization Bounds
May 23, 2021



Abstract:Heavy-tailed distributions have been studied in statistics, random matrix theory, physics, and econometrics as models of correlated systems, among other domains. Further, heavy-tail distributed eigenvalues of the covariance matrix of the weight matrices in neural networks have been shown to empirically correlate with test set accuracy in several works (e.g. arXiv:1901.08276), but a formal relationship between heavy-tail distributed parameters and generalization bounds was yet to be demonstrated. In this work, the compression framework of arXiv:1802.05296 is utilized to show that matrices with heavy-tail distributed matrix elements can be compressed, resulting in networks with sparse weight matrices. Since the parameter count has been reduced to a sum of the non-zero elements of sparse matrices, the compression framework allows us to bound the generalization gap of the resulting compressed network with a non-vacuous generalization bound. Further, the action of these matrices on a vector is discussed, and how they may relate to compression and resilient classification is analyzed.
An Energy-Based View of Graph Neural Networks
Apr 27, 2021



Abstract:Graph neural networks are a popular variant of neural networks that work with graph-structured data. In this work, we consider combining graph neural networks with the energy-based view of Grathwohl et al. (2019) with the aim of obtaining a more robust classifier. We successfully implement this framework by proposing a novel method to ensure generation over features as well as the adjacency matrix and evaluate our method against the standard graph convolutional network (GCN) architecture (Kipf & Welling (2016)). Our approach obtains comparable discriminative performance while improving robustness, opening promising new directions for future research for energy-based graph neural networks.
Dictionary Learning in Fourier Transform Scanning Tunneling Spectroscopy
Jul 19, 2018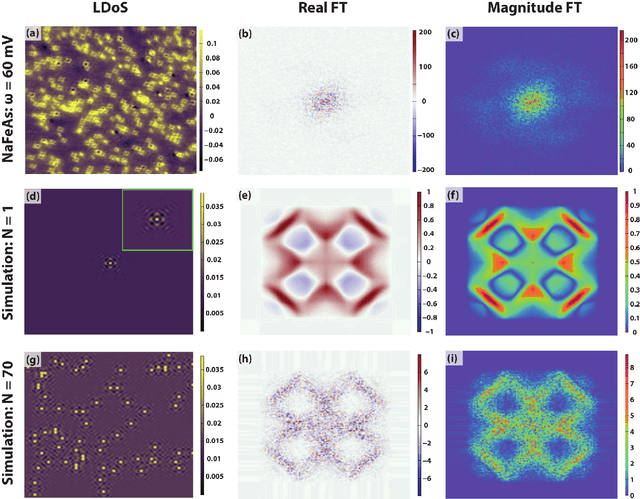
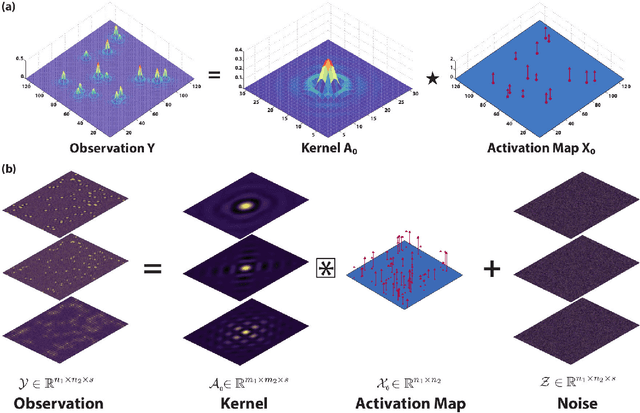
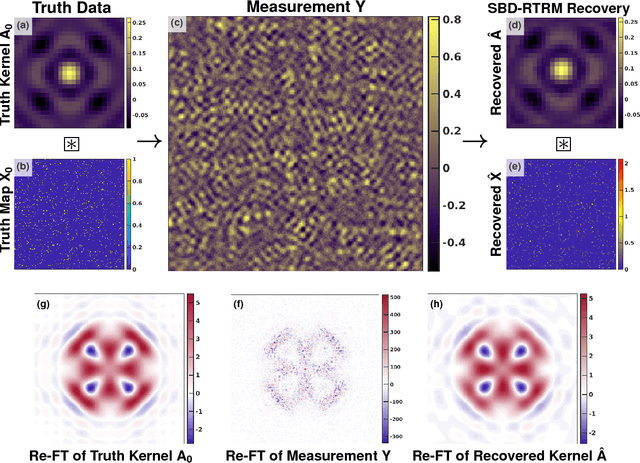
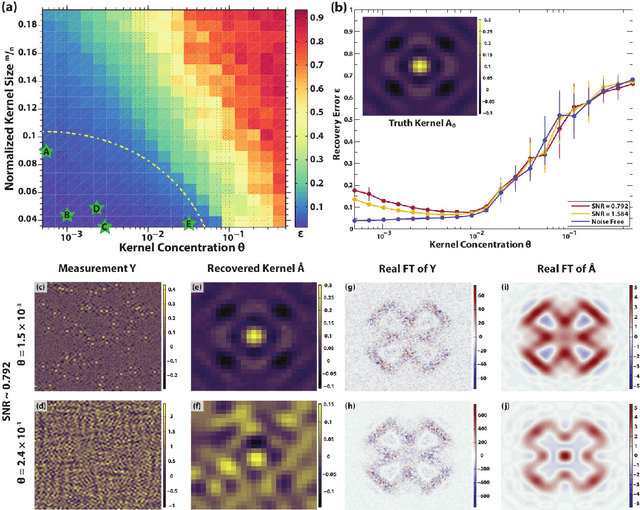
Abstract:Modern high-resolution microscopes, such as the scanning tunneling microscope, are commonly used to study specimens that have dense and aperiodic spatial structure. Extracting meaningful information from images obtained from such microscopes remains a formidable challenge. Fourier analysis is commonly used to analyze the underlying structure of fundamental motifs present in an image. However, the Fourier transform fundamentally suffers from severe phase noise when applied to aperiodic images. Here, we report the development of a new algorithm based on nonconvex optimization, applicable to any microscopy modality, that directly uncovers the fundamental motifs present in a real-space image. Apart from being quantitatively superior to traditional Fourier analysis, we show that this novel algorithm also uncovers phase sensitive information about the underlying motif structure. We demonstrate its usefulness by studying scanning tunneling microscopy images of a Co-doped iron arsenide superconductor and prove that the application of the algorithm allows for the complete recovery of quasiparticle interference in this material. Our phase sensitive quasiparticle interference imaging results indicate that the pairing symmetry in optimally doped NaFeAs is consistent with a sign-changing s+- order parameter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge