Koopman-based Deep Learning for Nonlinear System Estimation

Nonlinear differential equations are encountered as models of fluid flow, spiking neurons, and many other systems of interest in the real world. Common features of these systems are that their behaviors are difficult to describe exactly and invariably unmodeled dynamics present challenges in making precise predictions. In many cases the models exhibit extremely complicated behavior due to bifurcations and chaotic regimes. In this paper, we present a novel data-driven linear estimator that uses Koopman operator theory to extract finite-dimensional representations of complex nonlinear systems. The extracted model is used together with a deep reinforcement learning network that learns the optimal stepwise actions to predict future states of the original nonlinear system. Our estimator is also adaptive to a diffeomorphic transformation of the nonlinear system which enables transfer learning to compute state estimates of the transformed system without relearning from scratch.

Emulation Learning for Neuromimetic Systems

Building on our recent research on neural heuristic quantization systems, results on learning quantized motions and resilience to channel dropouts are reported. We propose a general emulation problem consistent with the neuromimetic paradigm. This optimal quantization problem can be solved by model predictive control (MPC), but because the optimization step involves integer programming, the approach suffers from combinatorial complexity when the number of input channels becomes large. Even if we collect data points to train a neural network simultaneously, collection of training data and the training itself are still time-consuming. Therefore, we propose a general Deep Q Network (DQN) algorithm that can not only learn the trajectory but also exhibit the advantages of resilience to channel dropout. Furthermore, to transfer the model to other emulation problems, a mapping-based transfer learning approach can be used directly on the current model to obtain the optimal direction for the new emulation problems.

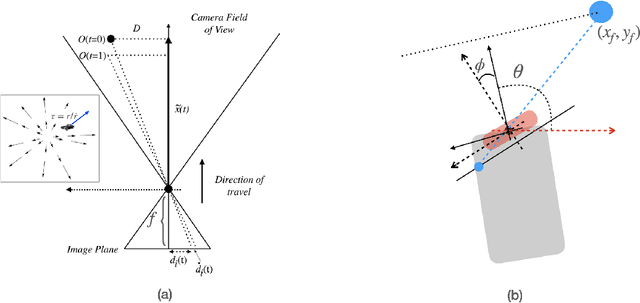
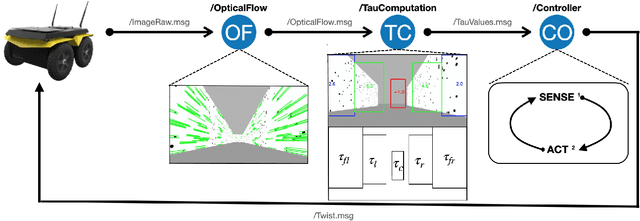
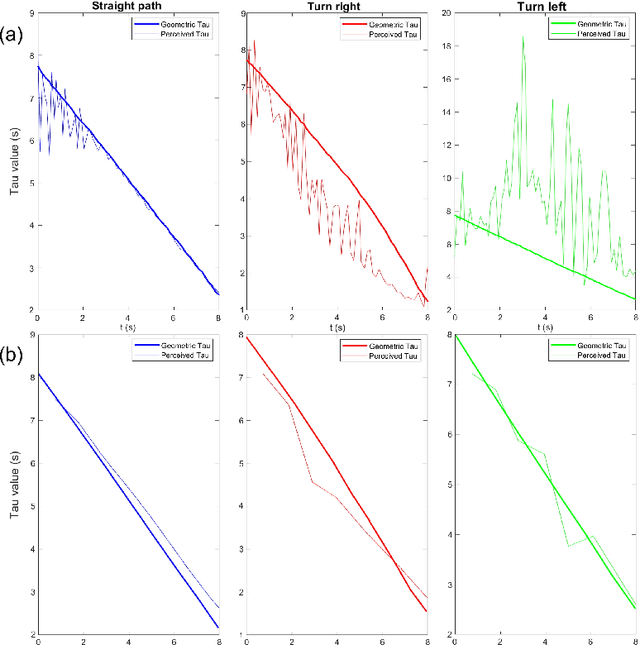
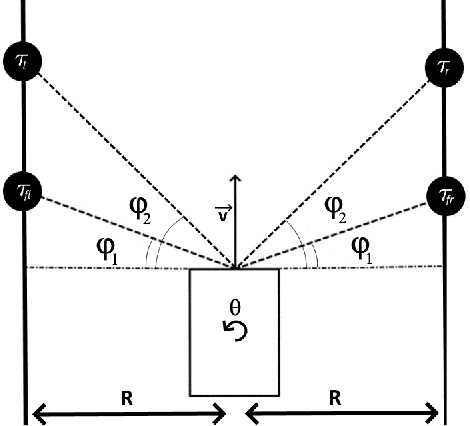
Visual Navigation Using Sparse Optical Flow and Time-to-Transit

Drawing inspiration from biology, we describe the way in which visual sensing with a monocular camera can provide a reliable signal for navigation of mobile robots. The work takes inspiration from a classic paper by Lee and Reddish (Nature, 1981, https://doi.org/10.1038/293293a0) in which they outline a behavioral strategy pursued by diving sea birds based on a visual cue called time-to-contact. A closely related concept of time-to-transit, tau, is defined, and it is shown that idealized steering laws based on monocular camera perceptions of tau can reliably and robustly steer a mobile vehicle within a wide variety of spaces in which features perceived to lie on walls and other objects in the environment provide adequate visual cues. The contribution of the paper is two-fold. It provides a simple theory of robust vision-based steering control. It goes on to show how the theory guides the implementation of robust visual navigation using ROS-Gazebo simulations as well as deployment and experiments with a camera-equipped Jackal robot. As far as we know, the experiments described below are the first to demonstrate visual navigation based on tau.

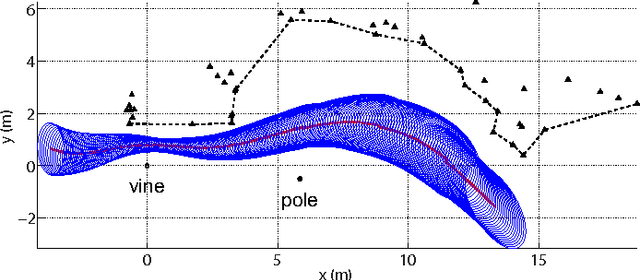
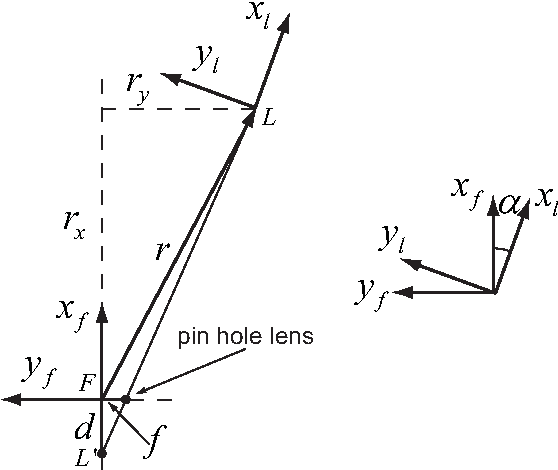
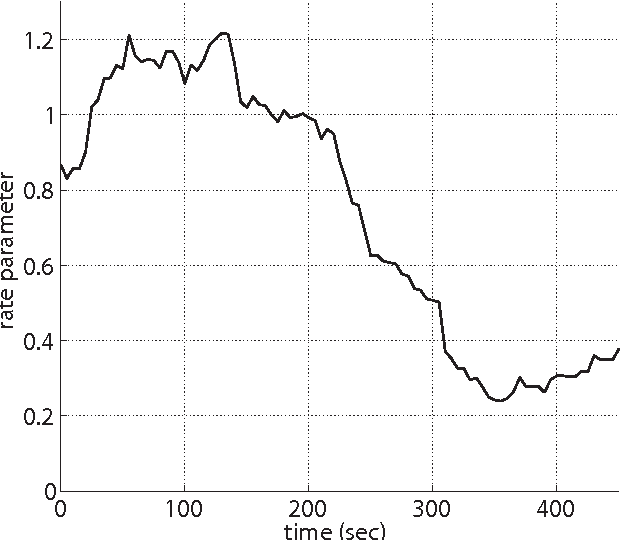
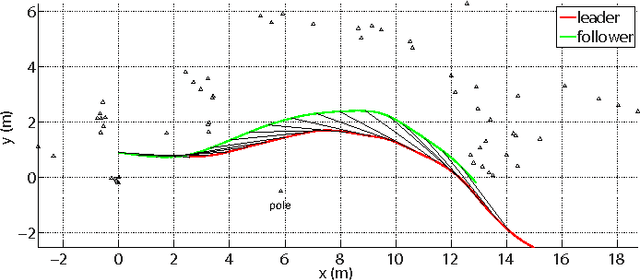
Perception and Steering Control in Paired Bat Flight

Animals within groups need to coordinate their reactions to perceived environmental features and to each other in order to safely move from one point to another. This paper extends our previously published work on the flight patterns of Myotis velifer that have been observed in a habitat near Johnson City, Texas. Each evening, these bats emerge from a cave in sequences of small groups that typically contain no more than three or four individuals, and they thus provide ideal subjects for studying leader-follower behaviors. By analyzing the flight paths of a group of M. velifer, the data show that the flight behavior of a follower bat is influenced by the flight behavior of a leader bat in a way that is not well explained by existing pursuit laws, such as classical pursuit, constant bearing and motion camouflage. Thus we propose an alternative steering law based on virtual loom, a concept we introduce to capture the geometrical configuration of the leader-follower pair. It is shown that this law may be integrated with our previously proposed vision-enabled steering laws to synthesize trajectories, the statistics of which fit with those of the bats in our data set. The results suggest that bats use perceived information of both the environment and their neighbors for navigation.