A Bayesian Sampling Approach to Exploration in Reinforcement Learning

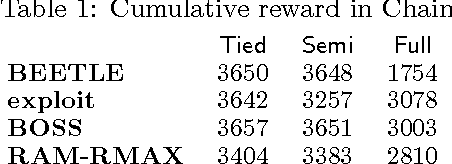
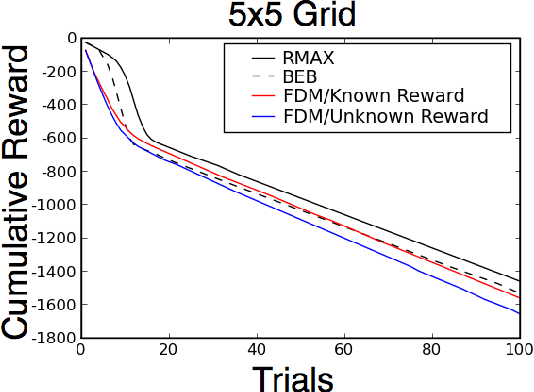
We present a modular approach to reinforcement learning that uses a Bayesian representation of the uncertainty over models. The approach, BOSS (Best of Sampled Set), drives exploration by sampling multiple models from the posterior and selecting actions optimistically. It extends previous work by providing a rule for deciding when to resample and how to combine the models. We show that our algorithm achieves nearoptimal reward with high probability with a sample complexity that is low relative to the speed at which the posterior distribution converges during learning. We demonstrate that BOSS performs quite favorably compared to state-of-the-art reinforcement-learning approaches and illustrate its flexibility by pairing it with a non-parametric model that generalizes across states.

Learning is planning: near Bayes-optimal reinforcement learning via Monte-Carlo tree search

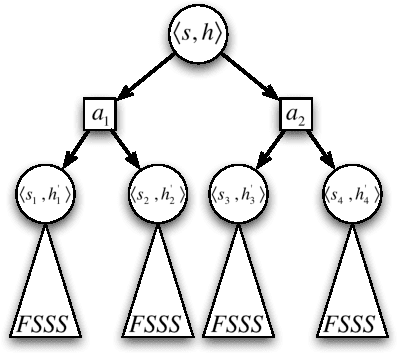
Bayes-optimal behavior, while well-defined, is often difficult to achieve. Recent advances in the use of Monte-Carlo tree search (MCTS) have shown that it is possible to act near-optimally in Markov Decision Processes (MDPs) with very large or infinite state spaces. Bayes-optimal behavior in an unknown MDP is equivalent to optimal behavior in the known belief-space MDP, although the size of this belief-space MDP grows exponentially with the amount of history retained, and is potentially infinite. We show how an agent can use one particular MCTS algorithm, Forward Search Sparse Sampling (FSSS), in an efficient way to act nearly Bayes-optimally for all but a polynomial number of steps, assuming that FSSS can be used to act efficiently in any possible underlying MDP.