Learning is planning: near Bayes-optimal reinforcement learning via Monte-Carlo tree search
Paper and Code
Feb 14, 2012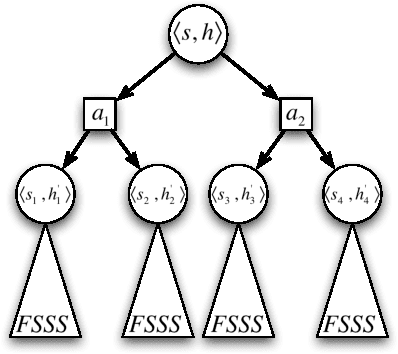
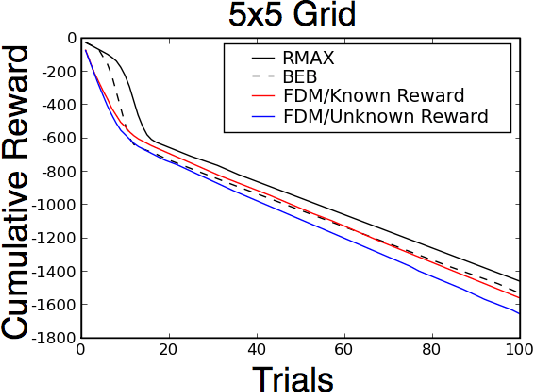

Bayes-optimal behavior, while well-defined, is often difficult to achieve. Recent advances in the use of Monte-Carlo tree search (MCTS) have shown that it is possible to act near-optimally in Markov Decision Processes (MDPs) with very large or infinite state spaces. Bayes-optimal behavior in an unknown MDP is equivalent to optimal behavior in the known belief-space MDP, although the size of this belief-space MDP grows exponentially with the amount of history retained, and is potentially infinite. We show how an agent can use one particular MCTS algorithm, Forward Search Sparse Sampling (FSSS), in an efficient way to act nearly Bayes-optimally for all but a polynomial number of steps, assuming that FSSS can be used to act efficiently in any possible underlying MDP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge