Structured Convolution Matrices for Energy-efficient Deep learning

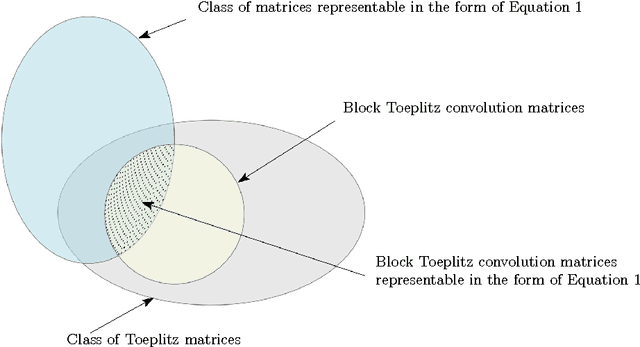
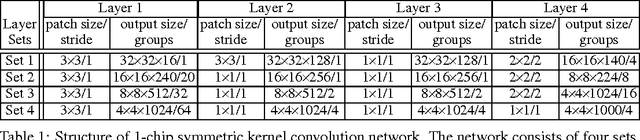
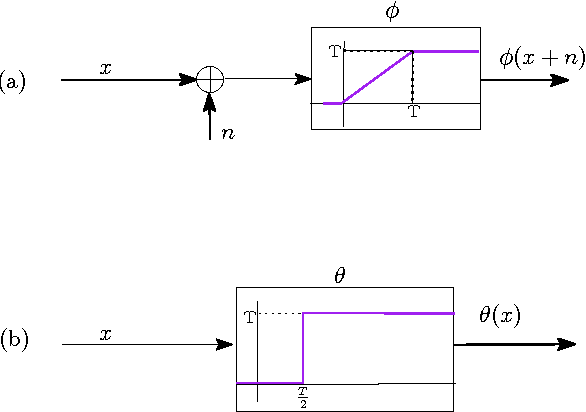
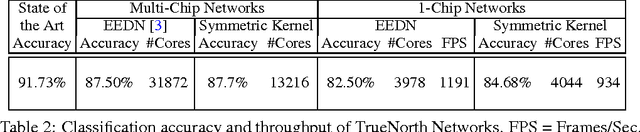
We derive a relationship between network representation in energy-efficient neuromorphic architectures and block Toplitz convolutional matrices. Inspired by this connection, we develop deep convolutional networks using a family of structured convolutional matrices and achieve state-of-the-art trade-off between energy efficiency and classification accuracy for well-known image recognition tasks. We also put forward a novel method to train binary convolutional networks by utilising an existing connection between noisy-rectified linear units and binary activations.

Deep neural networks are robust to weight binarization and other non-linear distortions

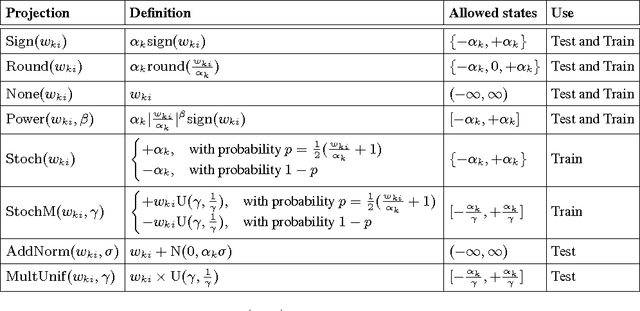
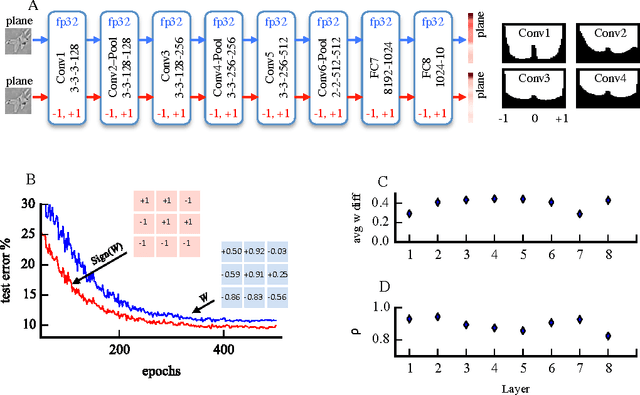
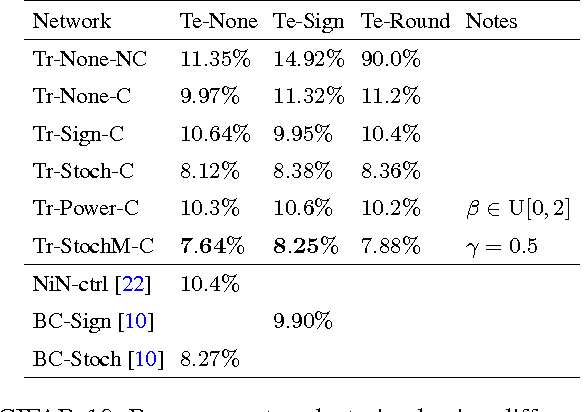
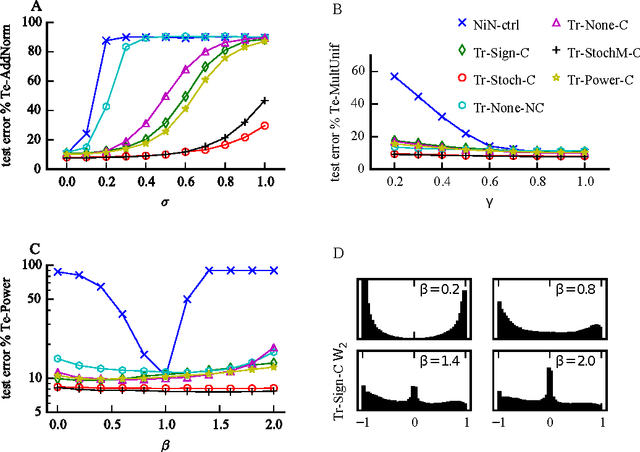
Recent results show that deep neural networks achieve excellent performance even when, during training, weights are quantized and projected to a binary representation. Here, we show that this is just the tip of the iceberg: these same networks, during testing, also exhibit a remarkable robustness to distortions beyond quantization, including additive and multiplicative noise, and a class of non-linear projections where binarization is just a special case. To quantify this robustness, we show that one such network achieves 11% test error on CIFAR-10 even with 0.68 effective bits per weight. Furthermore, we find that a common training heuristic--namely, projecting quantized weights during backpropagation--can be altered (or even removed) and networks still achieve a base level of robustness during testing. Specifically, training with weight projections other than quantization also works, as does simply clipping the weights, both of which have never been reported before. We confirm our results for CIFAR-10 and ImageNet datasets. Finally, drawing from these ideas, we propose a stochastic projection rule that leads to a new state of the art network with 7.64% test error on CIFAR-10 using no data augmentation.

Gibbs Sampling with Low-Power Spiking Digital Neurons

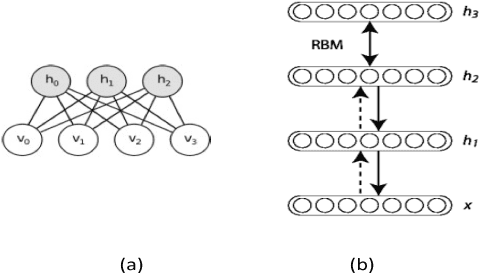
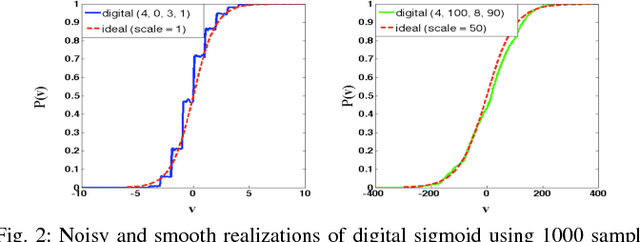
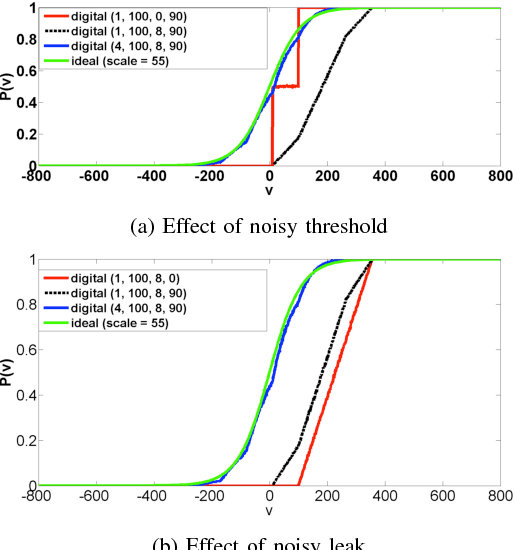
Restricted Boltzmann Machines and Deep Belief Networks have been successfully used in a wide variety of applications including image classification and speech recognition. Inference and learning in these algorithms uses a Markov Chain Monte Carlo procedure called Gibbs sampling. A sigmoidal function forms the kernel of this sampler which can be realized from the firing statistics of noisy integrate-and-fire neurons on a neuromorphic VLSI substrate. This paper demonstrates such an implementation on an array of digital spiking neurons with stochastic leak and threshold properties for inference tasks and presents some key performance metrics for such a hardware-based sampler in both the generative and discriminative contexts.

The thermodynamic temperature of a rhythmic spiking network

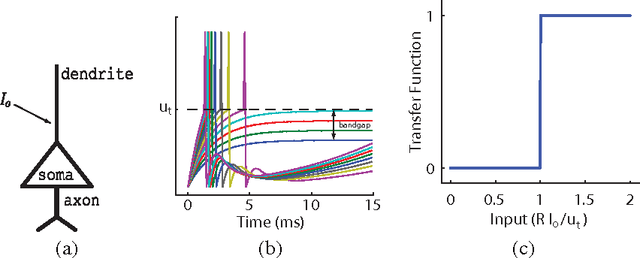
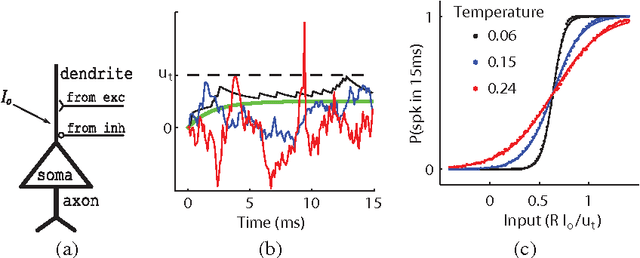
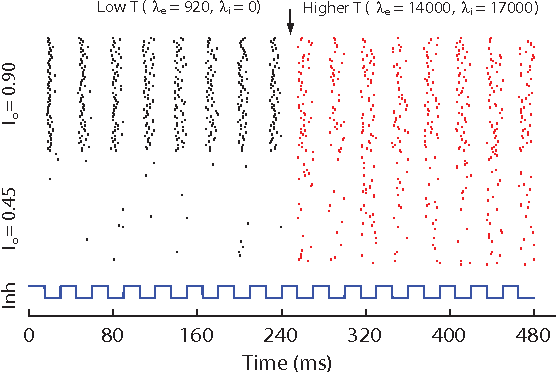
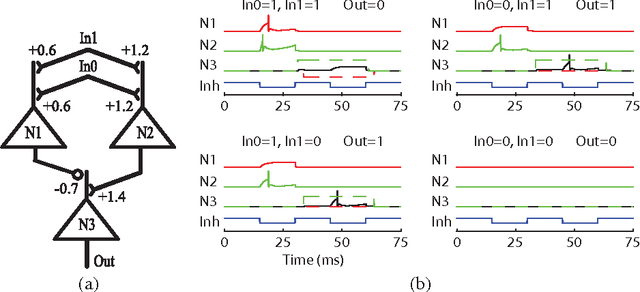
Artificial neural networks built from two-state neurons are powerful computational substrates, whose computational ability is well understood by analogy with statistical mechanics. In this work, we introduce similar analogies in the context of spiking neurons in a fixed time window, where excitatory and inhibitory inputs drawn from a Poisson distribution play the role of temperature. For single neurons with a "bandgap" between their inputs and the spike threshold, this temperature allows for stochastic spiking. By imposing a global inhibitory rhythm over the fixed time windows, we connect neurons into a network that exhibits synchronous, clock-like updating akin to neural networks. We implement a single-layer Boltzmann machine without learning to demonstrate our model.