Modelling crypto markets by multi-agent reinforcement learning

Building on a previous foundation work (Lussange et al. 2020), this study introduces a multi-agent reinforcement learning (MARL) model simulating crypto markets, which is calibrated to the Binance's daily closing prices of $153$ cryptocurrencies that were continuously traded between 2018 and 2022. Unlike previous agent-based models (ABM) or multi-agent systems (MAS) which relied on zero-intelligence agents or single autonomous agent methodologies, our approach relies on endowing agents with reinforcement learning (RL) techniques in order to model crypto markets. This integration is designed to emulate, with a bottom-up approach to complexity inference, both individual and collective agents, ensuring robustness in the recent volatile conditions of such markets and during the COVID-19 era. A key feature of our model also lies in the fact that its autonomous agents perform asset price valuation based on two sources of information: the market prices themselves, and the approximation of the crypto assets fundamental values beyond what those market prices are. Our MAS calibration against real market data allows for an accurate emulation of crypto markets microstructure and probing key market behaviors, in both the bearish and bullish regimes of that particular time period.

Continuous Time Continuous Space Homeostatic Reinforcement Learning (CTCS-HRRL) : Towards Biological Self-Autonomous Agent

Homeostasis is a biological process by which living beings maintain their internal balance. Previous research suggests that homeostasis is a learned behaviour. Recently introduced Homeostatic Regulated Reinforcement Learning (HRRL) framework attempts to explain this learned homeostatic behavior by linking Drive Reduction Theory and Reinforcement Learning. This linkage has been proven in the discrete time-space, but not in the continuous time-space. In this work, we advance the HRRL framework to a continuous time-space environment and validate the CTCS-HRRL (Continuous Time Continuous Space HRRL) framework. We achieve this by designing a model that mimics the homeostatic mechanisms in a real-world biological agent. This model uses the Hamilton-Jacobian Bellman Equation, and function approximation based on neural networks and Reinforcement Learning. Through a simulation-based experiment we demonstrate the efficacy of this model and uncover the evidence linked to the agent's ability to dynamically choose policies that favor homeostasis in a continuously changing internal-state milieu. Results of our experiments demonstrate that agent learns homeostatic behaviour in a CTCS environment, making CTCS-HRRL a promising framework for modellng animal dynamics and decision-making.

3D detection of roof sections from a single satellite image and application to LOD2-building reconstruction

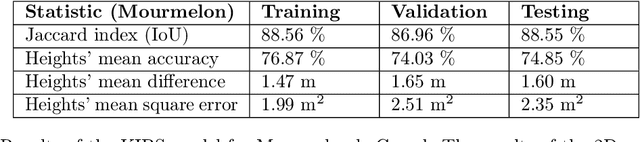
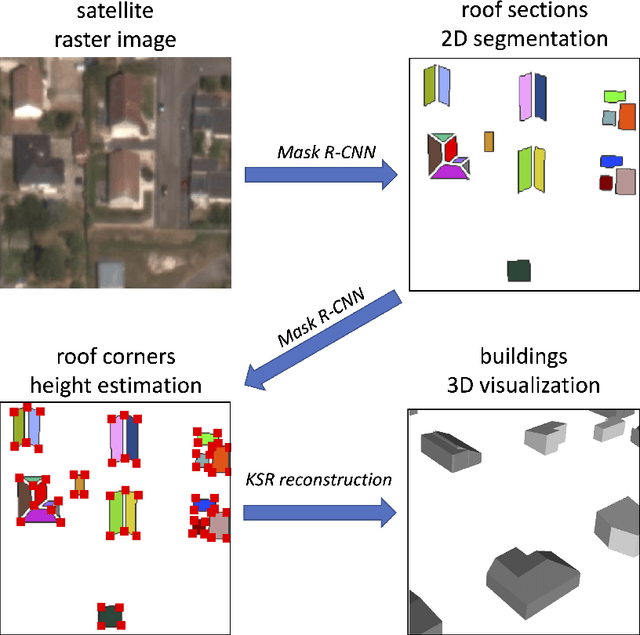
Reconstructing urban areas in 3D out of satellite raster images has been a long-standing and challenging goal of both academical and industrial research. The rare methods today achieving this objective at a Level Of Details $2$ rely on procedural approaches based on geometry, and need stereo images and/or LIDAR data as input. We here propose a method for urban 3D reconstruction named KIBS(\textit{Keypoints Inference By Segmentation}), which comprises two novel features: i) a full deep learning approach for the 3D detection of the roof sections, and ii) only one single (non-orthogonal) satellite raster image as model input. This is achieved in two steps: i) by a Mask R-CNN model performing a 2D segmentation of the buildings' roof sections, and after blending these latter segmented pixels within the RGB satellite raster image, ii) by another identical Mask R-CNN model inferring the heights-to-ground of the roof sections' corners via panoptic segmentation, unto full 3D reconstruction of the buildings and city. We demonstrate the potential of the KIBS method by reconstructing different urban areas in a few minutes, with a Jaccard index for the 2D segmentation of individual roof sections of $88.55\%$ and $75.21\%$ on our two data sets resp., and a height's mean error of such correctly segmented pixels for the 3D reconstruction of $1.60$ m and $2.06$ m on our two data sets resp., hence within the LOD2 precision range.

Continuous Homeostatic Reinforcement Learning for Self-Regulated Autonomous Agents

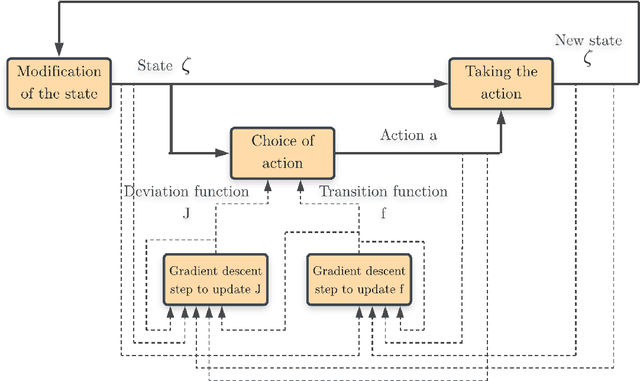
Homeostasis is a prevalent process by which living beings maintain their internal milieu around optimal levels. Multiple lines of evidence suggest that living beings learn to act to predicatively ensure homeostasis (allostasis). A classical theory for such regulation is drive reduction, where a function of the difference between the current and the optimal internal state. The recently introduced homeostatic regulated reinforcement learning theory (HRRL), by defining within the framework of reinforcement learning a reward function based on the internal state of the agent, makes the link between the theories of drive reduction and reinforcement learning. The HRRL makes it possible to explain multiple eating disorders. However, the lack of continuous change in the internal state of the agent with the discrete-time modeling has been so far a key shortcoming of the HRRL theory. Here, we propose an extension of the homeostatic reinforcement learning theory to a continuous environment in space and time, while maintaining the validity of the theoretical results and the behaviors explained by the model in discrete time. Inspired by the self-regulating mechanisms abundantly present in biology, we also introduce a model for the dynamics of the agent internal state, requiring the agent to continuously take actions to maintain homeostasis. Based on the Hamilton-Jacobi-Bellman equation and function approximation with neural networks, we derive a numerical scheme allowing the agent to learn directly how its internal mechanism works, and to choose appropriate action policies via reinforcement learning and an appropriate exploration of the environment. Our numerical experiments show that the agent does indeed learn to behave in a way that is beneficial to its survival in the environment, making our framework promising for modeling animal dynamics and decision-making.