Explicit Density Approximation for Neural Implicit Samplers Using a Bernstein-Based Convex Divergence

Rank-based statistical metrics, such as the invariant statistical loss (ISL), have recently emerged as robust and practically effective tools for training implicit generative models. In this work, we introduce dual-ISL, a novel likelihood-free objective for training implicit generative models that interchanges the roles of the target and model distributions in the ISL framework, yielding a convex optimization problem in the space of model densities. We prove that the resulting rank-based discrepancy $d_K$ is i) continuous under weak convergence and with respect to the $L^1$ norm, and ii) convex in its first argument-properties not shared by classical divergences such as KL or Wasserstein distances. Building on this, we develop a theoretical framework that interprets $d_K$ as an $L^2$-projection of the density ratio $q = p/\tilde p$ onto a Bernstein polynomial basis, from which we derive exact bounds on the truncation error, precise convergence rates, and a closed-form expression for the truncated density approximation. We further extend our analysis to the multivariate setting via random one-dimensional projections, defining a sliced dual-ISL divergence that retains both convexity and continuity. We empirically show that these theoretical advantages translate into practical ones. Specifically, across several benchmarks dual-ISL converges more rapidly, delivers markedly smoother and more stable training, and more effectively prevents mode collapse than classical ISL and other leading implicit generative methods-while also providing an explicit density approximation.

Robust training of implicit generative models for multivariate and heavy-tailed distributions with an invariant statistical loss

Traditional implicit generative models are capable of learning highly complex data distributions. However, their training involves distinguishing real data from synthetically generated data using adversarial discriminators, which can lead to unstable training dynamics and mode dropping issues. In this work, we build on the \textit{invariant statistical loss} (ISL) method introduced in \cite{de2024training}, and extend it to handle heavy-tailed and multivariate data distributions. The data generated by many real-world phenomena can only be properly characterised using heavy-tailed probability distributions, and traditional implicit methods struggle to effectively capture their asymptotic behavior. To address this problem, we introduce a generator trained with ISL, that uses input noise from a generalised Pareto distribution (GPD). We refer to this generative scheme as Pareto-ISL for conciseness. Our experiments demonstrate that Pareto-ISL accurately models the tails of the distributions while still effectively capturing their central characteristics. The original ISL function was conceived for 1D data sets. When the actual data is $n$-dimensional, a straightforward extension of the method was obtained by targeting the $n$ marginal distributions of the data. This approach is computationally infeasible and ineffective in high-dimensional spaces. To overcome this, we extend the 1D approach using random projections and define a new loss function suited for multivariate data, keeping problems tractable by adjusting the number of projections. We assess its performance in multidimensional generative modeling and explore its potential as a pretraining technique for generative adversarial networks (GANs) to prevent mode collapse, reporting promising results and highlighting its robustness across various hyperparameter settings.

Training Implicit Generative Models via an Invariant Statistical Loss

Implicit generative models have the capability to learn arbitrary complex data distributions. On the downside, training requires telling apart real data from artificially-generated ones using adversarial discriminators, leading to unstable training and mode-dropping issues. As reported by Zahee et al. (2017), even in the one-dimensional (1D) case, training a generative adversarial network (GAN) is challenging and often suboptimal. In this work, we develop a discriminator-free method for training one-dimensional (1D) generative implicit models and subsequently expand this method to accommodate multivariate cases. Our loss function is a discrepancy measure between a suitably chosen transformation of the model samples and a uniform distribution; hence, it is invariant with respect to the true distribution of the data. We first formulate our method for 1D random variables, providing an effective solution for approximate reparameterization of arbitrary complex distributions. Then, we consider the temporal setting (both univariate and multivariate), in which we model the conditional distribution of each sample given the history of the process. We demonstrate through numerical simulations that this new method yields promising results, successfully learning true distributions in a variety of scenarios and mitigating some of the well-known problems that state-of-the-art implicit methods present.

Convergence rates for optimised adaptive importance samplers

Adaptive importance samplers are adaptive Monte Carlo algorithms to estimate expectations with respect to some target distribution which adapt themselves to obtain better estimators over iterations. Although it is straightforward to show that they have the same $\mathcal{O}(1/\sqrt{N})$ convergence rate as the importance sampling where $N$ is the number of Monte Carlo samples, the behaviour of adaptive importance samplers over the number of iterations has been left relatively unexplored despite these adaptive algorithms aim at improving the proposal quality iteratively. In this work, we explore an adaptation strategy based on convex optimisation which leads to a class of adaptive importance samplers, termed optimised adaptive importance samplers (OAIS). These samplers rely on an adaptation idea based on minimizing the $\chi^2$-divergence between an exponential family proposal and the target. The analysed algorithms are closely related to the adaptive importance samplers which minimise the variance of the weight function. We first prove non-asymptotic error bounds for the mean squared errors (MSEs) of these algorithms, which explicitly depend on the number of iterations and the number of particles together. The non-asymptotic bounds derived in this paper imply that when the target is from the exponential family, the $L_2$ errors of the optimised samplers converge to the perfect Monte Carlo sampling error $\mathcal{O}(1/\sqrt{N})$. We also show that when the target is not from the exponential family, the asymptotic error rate is $\mathcal{O}(\sqrt{\rho^\star/N})$ where $\rho^\star$ is the minimum $\chi^2$-divergence between the target and an exponential family proposal.

A probabilistic incremental proximal gradient method

In this paper, we propose a probabilistic optimization method, named probabilistic incremental proximal gradient (PIPG) method, by developing a probabilistic interpretation of the incremental proximal gradient algorithm. We explicitly model the update rules of the incremental proximal gradient method and develop a systematic approach to propagate the uncertainty of the solution estimate over iterations. The PIPG algorithm takes the form of Bayesian filtering updates for a state-space model constructed by using the cost function. Our framework makes it possible to utilize well-known exact or approximate Bayesian filters, such as Kalman or extended Kalman filters, to solve large-scale regularized optimization problems.

Parallel sequential Monte Carlo for stochastic optimization

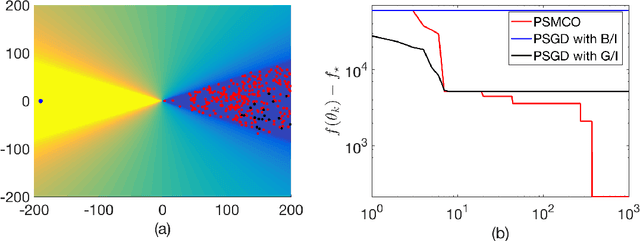
We propose a parallel sequential Monte Carlo optimization method to minimize cost functions which are computed as the sum of many component functions. The proposed scheme is a stochastic zeroth order optimization algorithm which uses only evaluations of small subsets of component functions to collect information from the problem. The algorithm consists of a bank of samplers and generates particle approximations of several sequences of probability measures. These measures are constructed in such a way that they have associated probability density functions whose global maxima coincide with the global minima of the cost function. The algorithm selects the best performing sampler and uses it to approximate a global minimum of the cost function. We prove analytically that the resulting estimator converges to a global minimum of the cost function almost surely as the number of Monte Carlo samples tends to infinity. We show that the algorithm can tackle cost functions with multiple minima or with wide flat regions.