Graphs in State-Space Models for Granger Causality in Climate Science

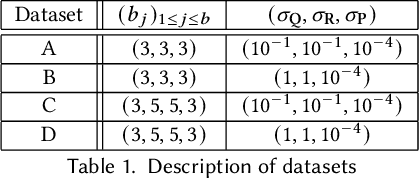
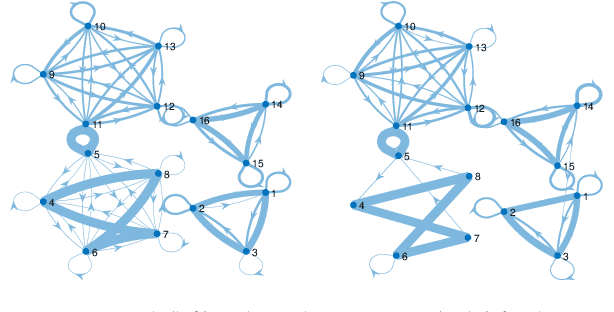
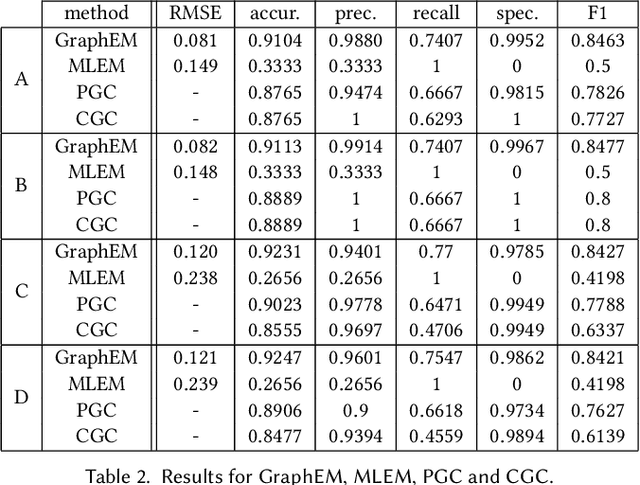
Granger causality (GC) is often considered not an actual form of causality. Still, it is arguably the most widely used method to assess the predictability of a time series from another one. Granger causality has been widely used in many applied disciplines, from neuroscience and econometrics to Earth sciences. We revisit GC under a graphical perspective of state-space models. For that, we use GraphEM, a recently presented expectation-maximisation algorithm for estimating the linear matrix operator in the state equation of a linear-Gaussian state-space model. Lasso regularisation is included in the M-step, which is solved using a proximal splitting Douglas-Rachford algorithm. Experiments in toy examples and challenging climate problems illustrate the benefits of the proposed model and inference technique over standard Granger causality methods.

A probabilistic incremental proximal gradient method

In this paper, we propose a probabilistic optimization method, named probabilistic incremental proximal gradient (PIPG) method, by developing a probabilistic interpretation of the incremental proximal gradient algorithm. We explicitly model the update rules of the incremental proximal gradient method and develop a systematic approach to propagate the uncertainty of the solution estimate over iterations. The PIPG algorithm takes the form of Bayesian filtering updates for a state-space model constructed by using the cost function. Our framework makes it possible to utilize well-known exact or approximate Bayesian filters, such as Kalman or extended Kalman filters, to solve large-scale regularized optimization problems.