Parallel sequential Monte Carlo for stochastic optimization

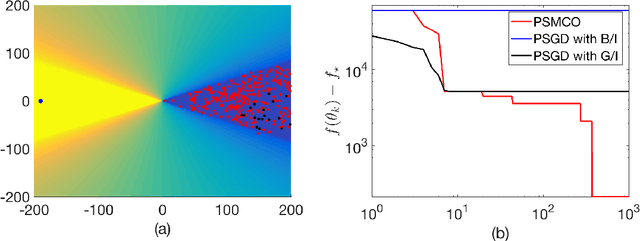
We propose a parallel sequential Monte Carlo optimization method to minimize cost functions which are computed as the sum of many component functions. The proposed scheme is a stochastic zeroth order optimization algorithm which uses only evaluations of small subsets of component functions to collect information from the problem. The algorithm consists of a bank of samplers and generates particle approximations of several sequences of probability measures. These measures are constructed in such a way that they have associated probability density functions whose global maxima coincide with the global minima of the cost function. The algorithm selects the best performing sampler and uses it to approximate a global minimum of the cost function. We prove analytically that the resulting estimator converges to a global minimum of the cost function almost surely as the number of Monte Carlo samples tends to infinity. We show that the algorithm can tackle cost functions with multiple minima or with wide flat regions.