Logistic $Q$-Learning

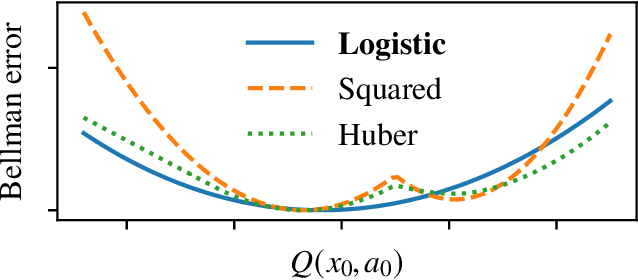
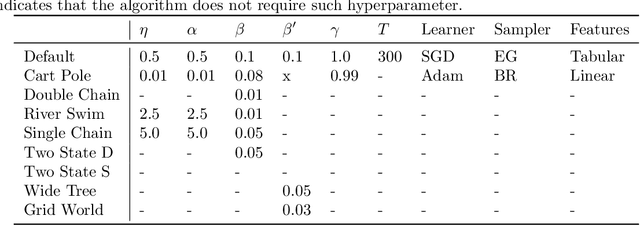
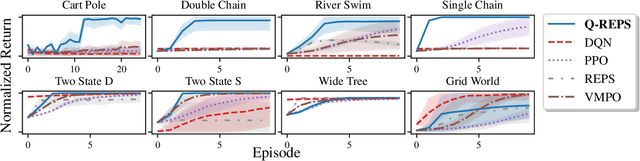
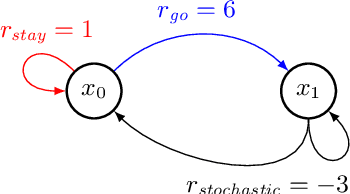
We propose a new reinforcement learning algorithm derived from a regularized linear-programming formulation of optimal control in MDPs. The method is closely related to the classic Relative Entropy Policy Search (REPS) algorithm of Peters et al. (2010), with the key difference that our method introduces a Q-function that enables efficient exact model-free implementation. The main feature of our algorithm (called QREPS) is a convex loss function for policy evaluation that serves as a theoretically sound alternative to the widely used squared Bellman error. We provide a practical saddle-point optimization method for minimizing this loss function and provide an error-propagation analysis that relates the quality of the individual updates to the performance of the output policy. Finally, we demonstrate the effectiveness of our method on a range of benchmark problems.

Faster saddle-point optimization for solving large-scale Markov decision processes

We consider the problem of computing optimal policies in average-reward Markov decision processes. This classical problem can be formulated as a linear program directly amenable to saddle-point optimization methods, albeit with a number of variables that is linear in the number of states. To address this issue, recent work has considered a linearly relaxed version of the resulting saddle-point problem. Our work aims at achieving a better understanding of this relaxed optimization problem by characterizing the conditions necessary for convergence to the optimal policy, and designing an optimization algorithm enjoying fast convergence rates that are independent of the size of the state space. Notably, our characterization points out some potential issues with previous work.