Faster saddle-point optimization for solving large-scale Markov decision processes
Paper and Code
Sep 22, 2019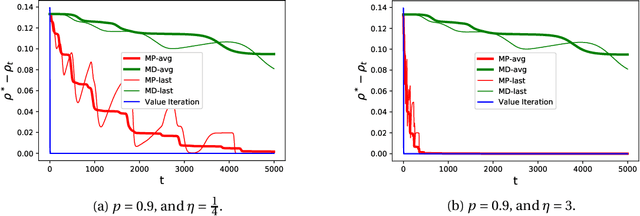
We consider the problem of computing optimal policies in average-reward Markov decision processes. This classical problem can be formulated as a linear program directly amenable to saddle-point optimization methods, albeit with a number of variables that is linear in the number of states. To address this issue, recent work has considered a linearly relaxed version of the resulting saddle-point problem. Our work aims at achieving a better understanding of this relaxed optimization problem by characterizing the conditions necessary for convergence to the optimal policy, and designing an optimization algorithm enjoying fast convergence rates that are independent of the size of the state space. Notably, our characterization points out some potential issues with previous work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge