Outlier-resilient model fitting via percentile losses: Methods for general and convex residuals

We consider the problem of robustly fitting a model to data that includes outliers by formulating a percentile optimization problem. This problem is non-smooth and non-convex, hence hard to solve. We derive properties that the minimizers of such problems must satisfy. These properties lead to methods that solve the percentile formulation both for general residuals and for convex residuals. The methods fit the model to subsets of the data, and then extract the solution of the percentile formulation from these partial fits. As illustrative simulations show, such methods endure higher outlier percentages, when compared with standard robust estimates. Additionally, the derived properties provide a broader and alternative theoretical validation for existing robust methods, whose validity was previously limited to specific forms of the residuals.

Robust Target Localization in 2D: A Value-at-Risk Approach

This paper consider considers the problem of locating a two dimensional target from range-measurements containing outliers. Assuming that the number of outlier is known, we formulate the problem of minimizing inlier losses while ignoring outliers. This leads to a combinatorial, non-convex, non-smooth problem involving the percentile function. Using the framework of risk analysis from Rockafellar et al., we start by interpreting this formulation as a Value-at-risk (VaR) problem from portfolio optimization. To the best of our knowledge, this is the first time that a localization problem was formulated using risk analysis theory. To study the VaR formulation, we start by designing a majorizer set that contains any solution of a general percentile problem. This set is useful because, when applied to a localization scenario in 2D, it allows to majorize the solution set in terms of singletons, circumferences, ellipses and hyperbolas. Using know parametrization of these curves, we propose a grid method for the original non-convex problem. So we reduce the task of optimizing the VaR objective to that of efficiently sampling the proposed majorizer set. We compare our algorithm with four benchmarks in target localization. Numerical simulations show that our method is fast while, on average, improving the accuracy of the best benchmarks by at least 100m in a 1 Km$^2$ area.

Distributed detection of ARMA signals

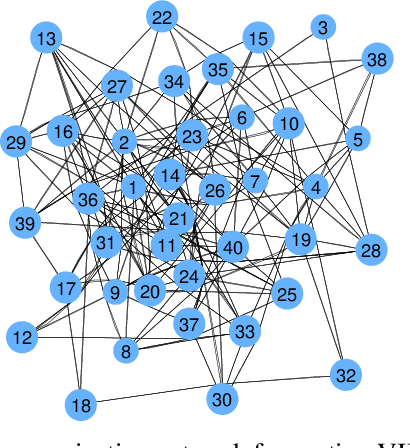
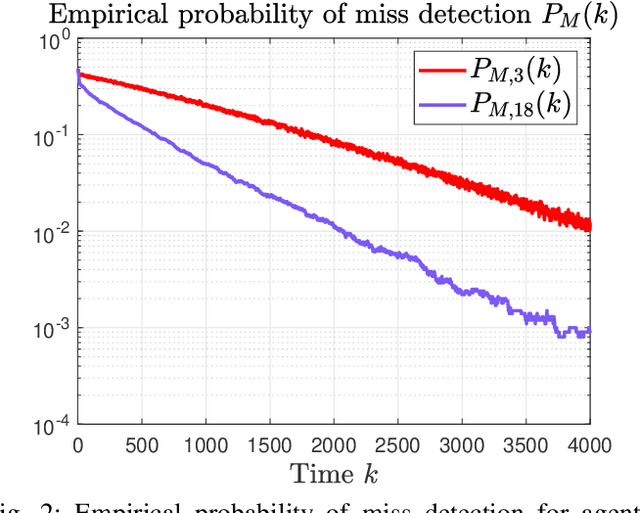
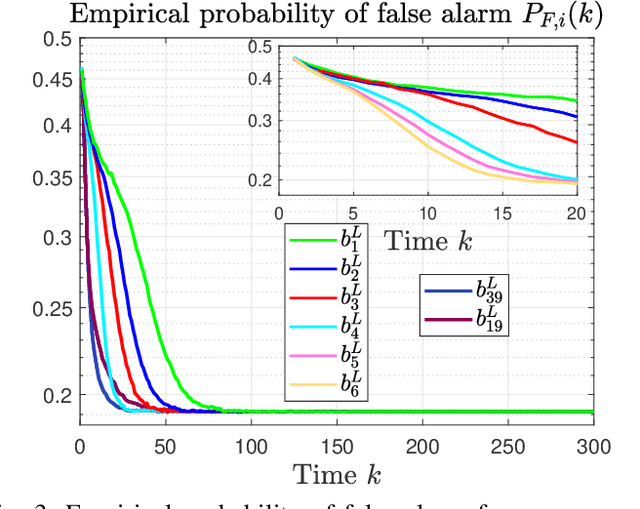
This paper considers a distributed detection setup where agents in a network want to detect a time-varying signal embedded in temporally correlated noise. The signal of interest is the impulse response of an ARMA (auto-regressive moving average) filter, and the noise is the output of yet another ARMA filter which is fed white Gaussian noise. For this extended problem setup, which can prompt novel behaviour, we propose a comprehensive solution. First, we extend the well-known running consensus detector (RCD) to this correlated setup; then, we design an efficient implementation of the RCD by exploiting the underlying ARMA structures; and, finally, we derive the theoretical asymptotic performance of the RCD in this ARMA setup. It turns out that the error probability at each agent exhibits one of two regimes: either (a) the error probability decays exponentially fast to zero or (b) it converges to a strictly positive error floor. While regime (a) spans staple results in large deviation theory, regime (b) is new in distributed detection and is elicited by the ARMA setup. We fully characterize these two scenarios: we give necessary and sufficient conditions, phrased in terms of the zero and poles of the underlying ARMA models, for the emergence of each regime, and provide closed-form expressions for both the decay rates of regime (a) and the positive error floors of regime (b). Our analysis also shows that the ARMA setup leads to two novel features: (1) the threshold level used in RCD can influence the asymptotics of the error probabilities and (2) some agents might be weakly informative, in the sense that their observations do not improve the asymptotic performance of RCD and, as such, can be safely muted to save sensing resources. Numerical simulations illustrate and confirm the theoretical findings.

Robust Localization with Bounded Noise: Creating a Superset of the Possible Target Positions via Linear-Fractional Representations

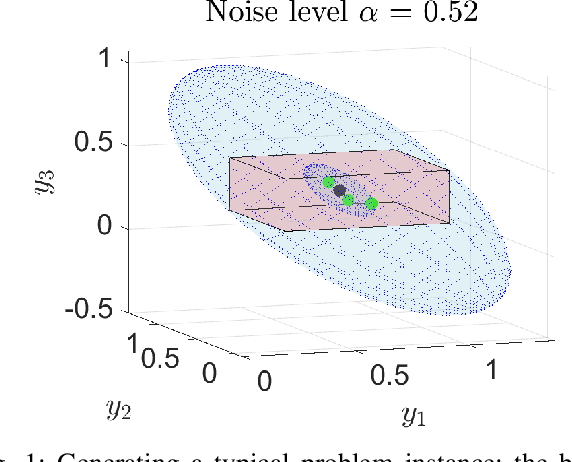
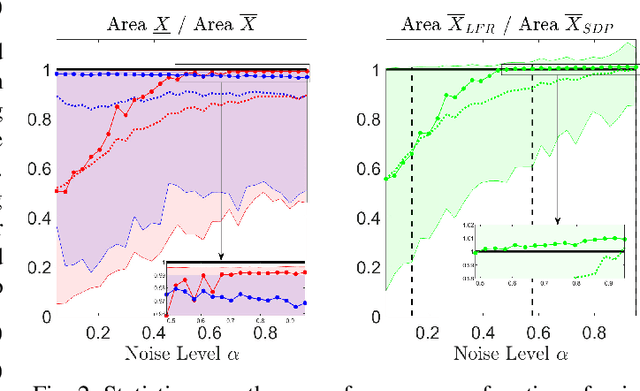
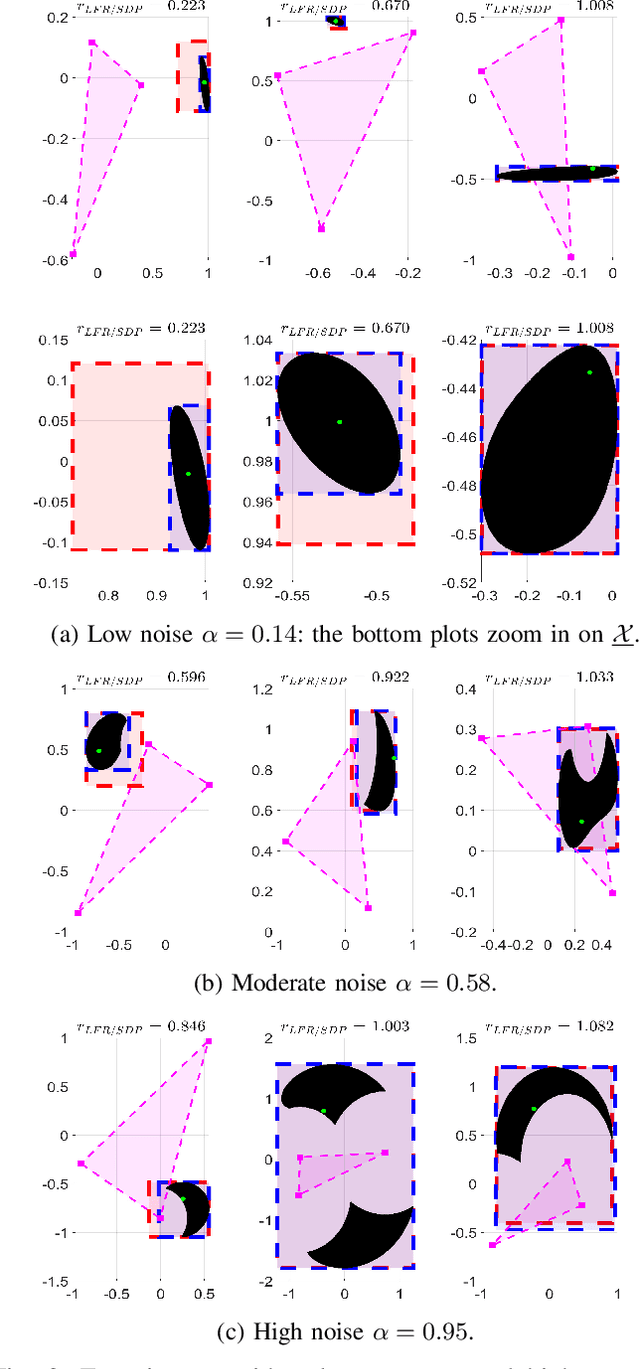
Locating an object is key in many applications, namely in high-stakes real-world scenarios, like detecting humans or obstacles in vehicular networks. In such applications, pointwise estimates are not enough, and the full area of locations compatible with acquired measurements should be available, for robust and safe navigation. This paper presents a scalable algorithm for creating a superset of all possible target locations, given range measurements with bounded error. The assumption of bounded error is mild, since both hardware characteristics and application scenario impose upper bounds on measurement errors, and the bounded set can be taken from confidence regions of the error distributions. We construct the superset through convex relaxations that use Linear Fractional Representations (LFRs), a well-known technique in robust control. Additionally, we also provide a statistical interpretation for the set of possible target positions, considering the framework of robust estimation. Finally, we provide empirical validation by comparing our LFR method with a standard semidefinite relaxation. Our approach has shown to pay off for small to moderate noise levels: the supersets created by our method are tighter than the benchmark ones being about 20% smaller in size. Furthermore, our method tends to be tight because the size of the supersets is, on median terms, within a 3% margin of a lower bound computed via grid search.