Distributed detection of ARMA signals
Paper and Code
Apr 14, 2023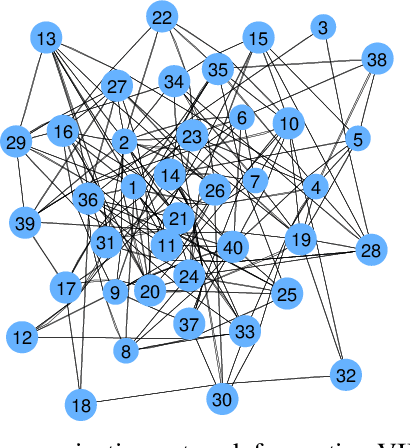
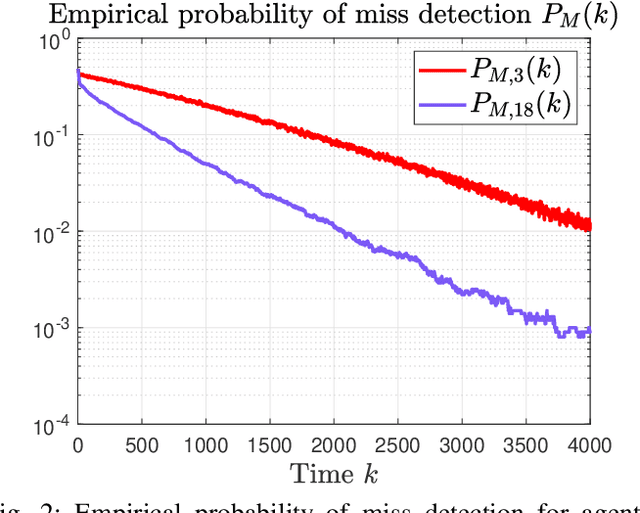
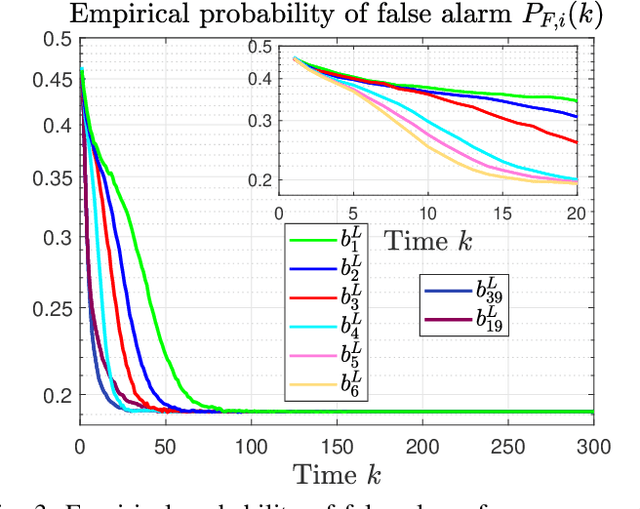
This paper considers a distributed detection setup where agents in a network want to detect a time-varying signal embedded in temporally correlated noise. The signal of interest is the impulse response of an ARMA (auto-regressive moving average) filter, and the noise is the output of yet another ARMA filter which is fed white Gaussian noise. For this extended problem setup, which can prompt novel behaviour, we propose a comprehensive solution. First, we extend the well-known running consensus detector (RCD) to this correlated setup; then, we design an efficient implementation of the RCD by exploiting the underlying ARMA structures; and, finally, we derive the theoretical asymptotic performance of the RCD in this ARMA setup. It turns out that the error probability at each agent exhibits one of two regimes: either (a) the error probability decays exponentially fast to zero or (b) it converges to a strictly positive error floor. While regime (a) spans staple results in large deviation theory, regime (b) is new in distributed detection and is elicited by the ARMA setup. We fully characterize these two scenarios: we give necessary and sufficient conditions, phrased in terms of the zero and poles of the underlying ARMA models, for the emergence of each regime, and provide closed-form expressions for both the decay rates of regime (a) and the positive error floors of regime (b). Our analysis also shows that the ARMA setup leads to two novel features: (1) the threshold level used in RCD can influence the asymptotics of the error probabilities and (2) some agents might be weakly informative, in the sense that their observations do not improve the asymptotic performance of RCD and, as such, can be safely muted to save sensing resources. Numerical simulations illustrate and confirm the theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge