Robust Target Localization in 2D: A Value-at-Risk Approach
Paper and Code
Jul 05, 2023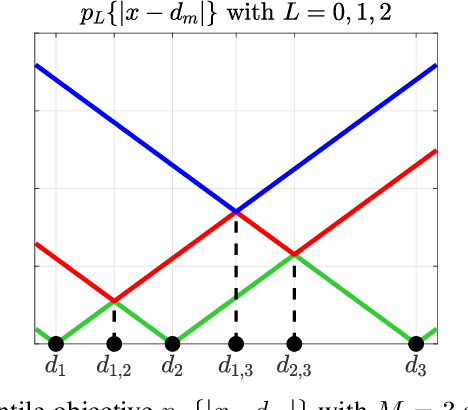
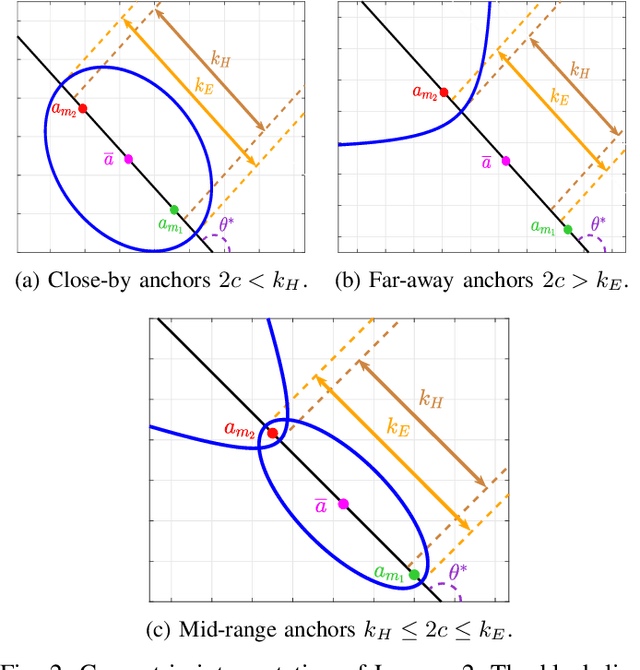
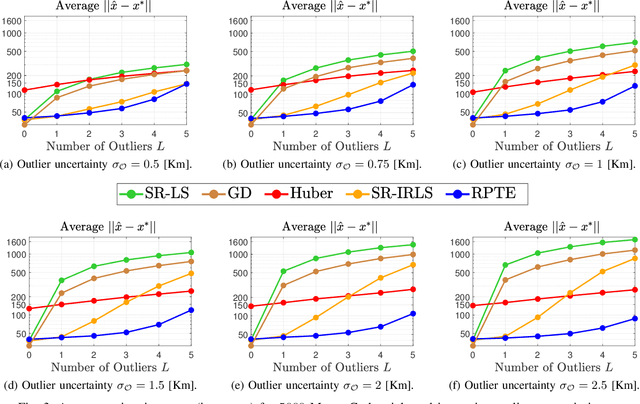
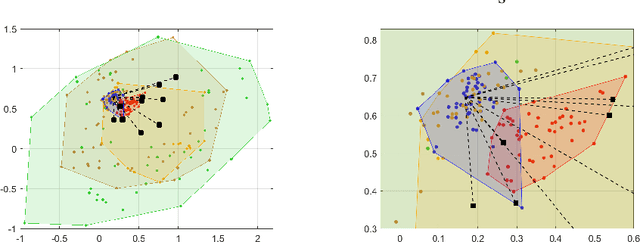
This paper consider considers the problem of locating a two dimensional target from range-measurements containing outliers. Assuming that the number of outlier is known, we formulate the problem of minimizing inlier losses while ignoring outliers. This leads to a combinatorial, non-convex, non-smooth problem involving the percentile function. Using the framework of risk analysis from Rockafellar et al., we start by interpreting this formulation as a Value-at-risk (VaR) problem from portfolio optimization. To the best of our knowledge, this is the first time that a localization problem was formulated using risk analysis theory. To study the VaR formulation, we start by designing a majorizer set that contains any solution of a general percentile problem. This set is useful because, when applied to a localization scenario in 2D, it allows to majorize the solution set in terms of singletons, circumferences, ellipses and hyperbolas. Using know parametrization of these curves, we propose a grid method for the original non-convex problem. So we reduce the task of optimizing the VaR objective to that of efficiently sampling the proposed majorizer set. We compare our algorithm with four benchmarks in target localization. Numerical simulations show that our method is fast while, on average, improving the accuracy of the best benchmarks by at least 100m in a 1 Km$^2$ area.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge