An Exact Solver for Satisfiability Modulo Counting with Probabilistic Circuits

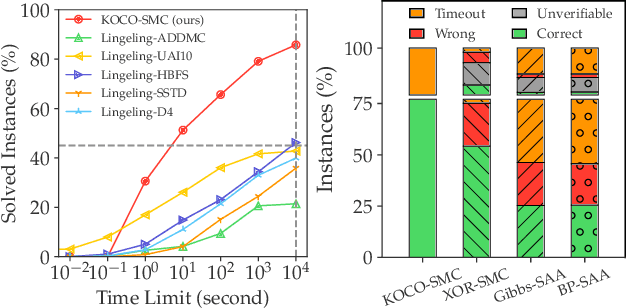
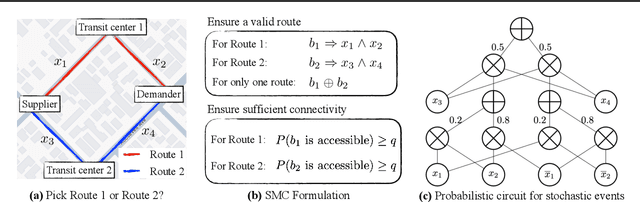
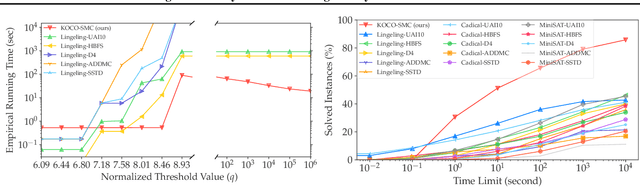
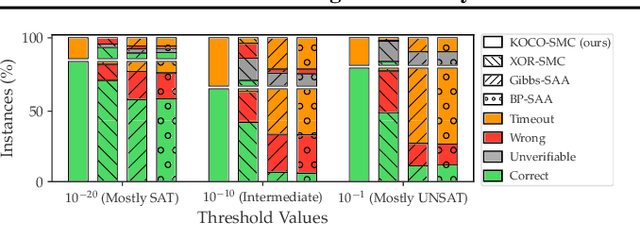
Satisfiability Modulo Counting (SMC) is a recently proposed general language to reason about problems integrating statistical and symbolic artificial intelligence. An SMC formula is an extended SAT formula in which the truth values of a few Boolean variables are determined by probabilistic inference. Existing approximate solvers optimize surrogate objectives, which lack formal guarantees. Current exact solvers directly integrate SAT solvers and probabilistic inference solvers resulting in slow performance because of many back-and-forth invocations of both solvers. We propose KOCO-SMC, an integrated exact SMC solver that efficiently tracks lower and upper bounds in the probabilistic inference process. It enhances computational efficiency by enabling early estimation of probabilistic inference using only partial variable assignments, whereas existing methods require full variable assignments. In the experiment, we compare KOCO-SMC with currently available approximate and exact SMC solvers on large-scale datasets and real-world applications. Our approach delivers high-quality solutions with high efficiency.

A Tighter Convergence Proof of Reverse Experience Replay

In reinforcement learning, Reverse Experience Replay (RER) is a recently proposed algorithm that attains better sample complexity than the classic experience replay method. RER requires the learning algorithm to update the parameters through consecutive state-action-reward tuples in reverse order. However, the most recent theoretical analysis only holds for a minimal learning rate and short consecutive steps, which converge slower than those large learning rate algorithms without RER. In view of this theoretical and empirical gap, we provide a tighter analysis that mitigates the limitation on the learning rate and the length of consecutive steps. Furthermore, we show theoretically that RER converges with a larger learning rate and a longer sequence.

Solving Satisfiability Modulo Counting for Symbolic and Statistical AI Integration With Provable Guarantees

Satisfiability Modulo Counting (SMC) encompasses problems that require both symbolic decision-making and statistical reasoning. Its general formulation captures many real-world problems at the intersection of symbolic and statistical Artificial Intelligence. SMC searches for policy interventions to control probabilistic outcomes. Solving SMC is challenging because of its highly intractable nature($\text{NP}^{\text{PP}}$-complete), incorporating statistical inference and symbolic reasoning. Previous research on SMC solving lacks provable guarantees and/or suffers from sub-optimal empirical performance, especially when combinatorial constraints are present. We propose XOR-SMC, a polynomial algorithm with access to NP-oracles, to solve highly intractable SMC problems with constant approximation guarantees. XOR-SMC transforms the highly intractable SMC into satisfiability problems, by replacing the model counting in SMC with SAT formulae subject to randomized XOR constraints. Experiments on solving important SMC problems in AI for social good demonstrate that XOR-SMC finds solutions close to the true optimum, outperforming several baselines which struggle to find good approximations for the intractable model counting in SMC.