Variational Wasserstein Barycenters with c-Cyclical Monotonicity

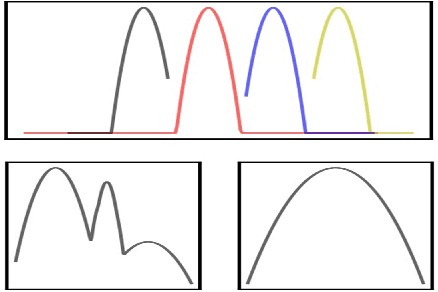
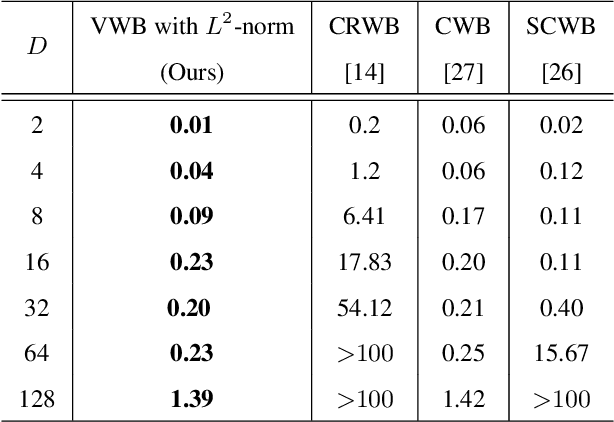
Wasserstein barycenter, built on the theory of optimal transport, provides a powerful framework to aggregate probability distributions, and it has increasingly attracted great attention within the machine learning community. However, it suffers from severe computational burden, especially for high dimensional and continuous settings. To this end, we develop a novel continuous approximation method for the Wasserstein barycenters problem given sample access to the input distributions. The basic idea is to introduce a variational distribution as the approximation of the true continuous barycenter, so as to frame the barycenters computation problem as an optimization problem, where parameters of the variational distribution adjust the proxy distribution to be similar to the barycenter. Leveraging the variational distribution, we construct a tractable dual formulation for the regularized Wasserstein barycenter problem with c-cyclical monotonicity, which can be efficiently solved by stochastic optimization. We provide theoretical analysis on convergence and demonstrate the practical effectiveness of our method on real applications of subset posterior aggregation and synthetic data.

Topic representation: finding more representative words in topic models

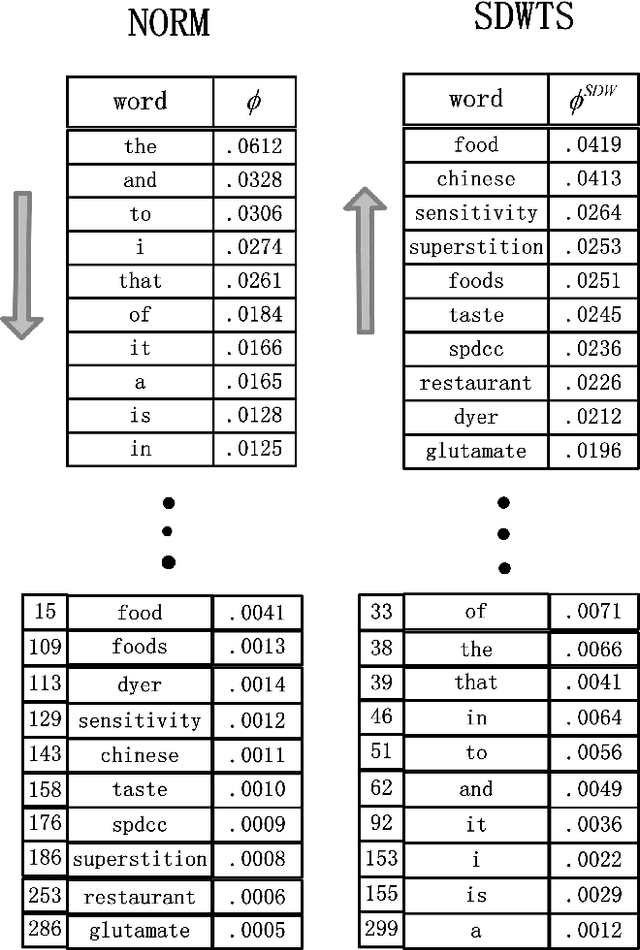
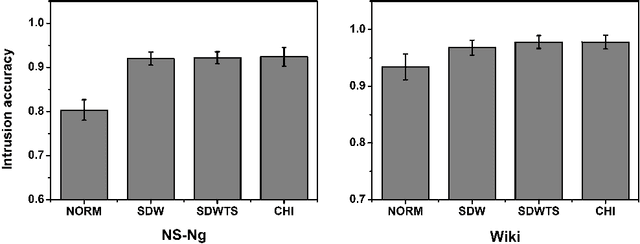
The top word list, i.e., the top-M words with highest marginal probability in a given topic, is the standard topic representation in topic models. Most of recent automatical topic labeling algorithms and popular topic quality metrics are based on it. However, we find, empirically, words in this type of top word list are not always representative. The objective of this paper is to find more representative top word lists for topics. To achieve this, we rerank the words in a given topic by further considering marginal probability on words over every other topic. The reranking list of top-M words is used to be a novel topic representation for topic models. We investigate three reranking methodologies, using (1) standard deviation weight, (2) standard deviation weight with topic size and (3) Chi Square \c{hi}2statistic selection. Experimental results on real world collections indicate that our representations can extract more representative words for topics, agreeing with human judgements.