mm-Wave Radar Hand Shape Classification Using Deformable Transformers

A novel, real-time, mm-Wave radar-based static hand shape classification algorithm and implementation are proposed. The method finds several applications in low cost and privacy sensitive touchless control technology using 60 Ghz radar as the sensor input. As opposed to prior Range-Doppler image based 2D classification solutions, our method converts raw radar data to 3D sparse cartesian point clouds.The demonstrated 3D radar neural network model using deformable transformers significantly surpasses the performance results set by prior methods which either utilize custom signal processing or apply generic convolutional techniques on Range-Doppler FFT images. Experiments are performed on an internally collected dataset using an off-the-shelf radar sensor.

Asymptotic Analysis of Sampling Estimators for Randomized Numerical Linear Algebra Algorithms

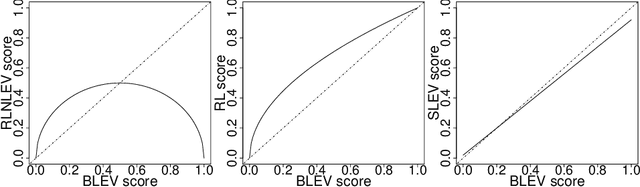
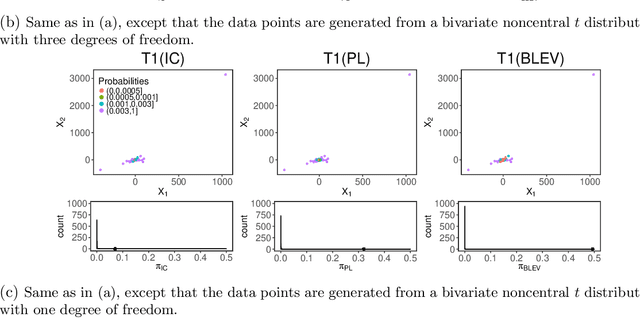
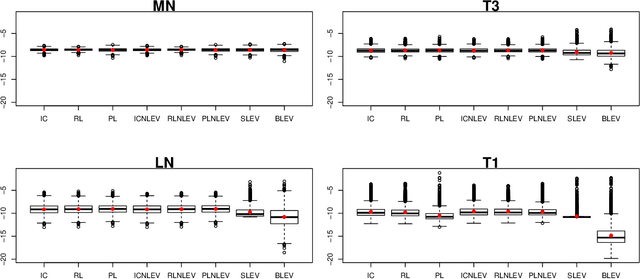
The statistical analysis of Randomized Numerical Linear Algebra (RandNLA) algorithms within the past few years has mostly focused on their performance as point estimators. However, this is insufficient for conducting statistical inference, e.g., constructing confidence intervals and hypothesis testing, since the distribution of the estimator is lacking. In this article, we develop an asymptotic analysis to derive the distribution of RandNLA sampling estimators for the least-squares problem. In particular, we derive the asymptotic distribution of a general sampling estimator with arbitrary sampling probabilities. The analysis is conducted in two complementary settings, i.e., when the objective of interest is to approximate the full sample estimator or is to infer the underlying ground truth model parameters. For each setting, we show that the sampling estimator is asymptotically normally distributed under mild regularity conditions. Moreover, the sampling estimator is asymptotically unbiased in both settings. Based on our asymptotic analysis, we use two criteria, the Asymptotic Mean Squared Error (AMSE) and the Expected Asymptotic Mean Squared Error (EAMSE), to identify optimal sampling probabilities. Several of these optimal sampling probability distributions are new to the literature, e.g., the root leverage sampling estimator and the predictor length sampling estimator. Our theoretical results clarify the role of leverage in the sampling process, and our empirical results demonstrate improvements over existing methods.

Communication-Efficient Distributed Estimator for Generalized Linear Models with a Diverging Number of Covariates

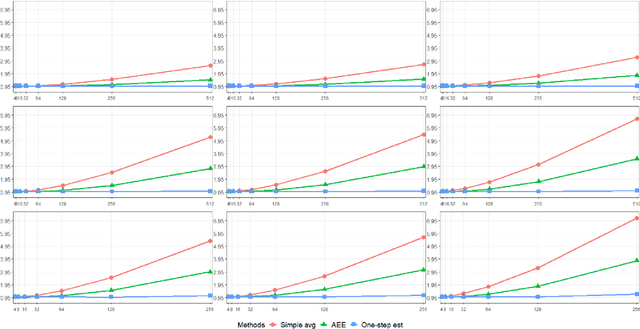
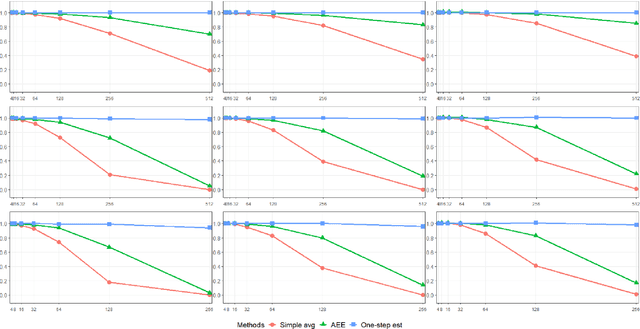
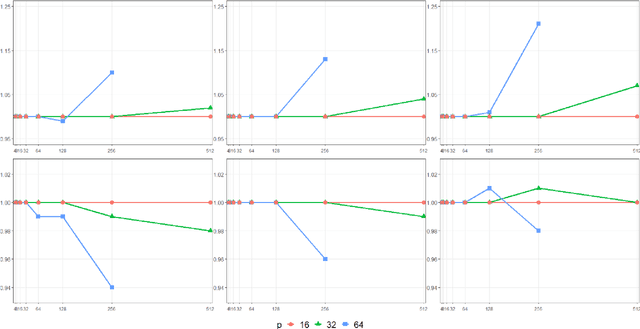
Distributed statistical inference has recently attracted immense attention. Herein, we study the asymptotic efficiency of the maximum likelihood estimator (MLE), the one-step MLE, and the aggregated estimating equation estimator for generalized linear models with a diverging number of covariates. Then a novel method is proposed to obtain an asymptotically efficient estimator for large-scale distributed data by two rounds of communication between local machines and the central server. The assumption on the number of machines in this paper is more relaxed and thus practical for real-world applications. Simulations and a case study demonstrate the satisfactory finite-sample performance of the proposed estimators.