SLIM: a Scalable Light-weight Root Cause Analysis for Imbalanced Data in Microservice

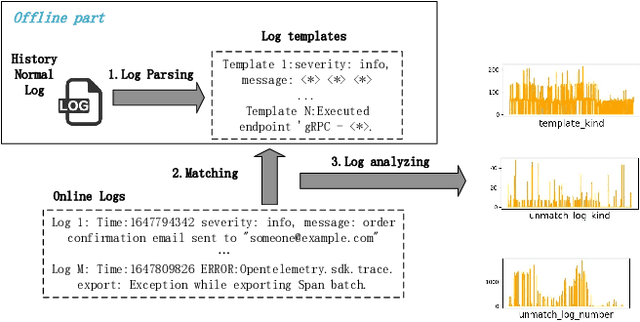
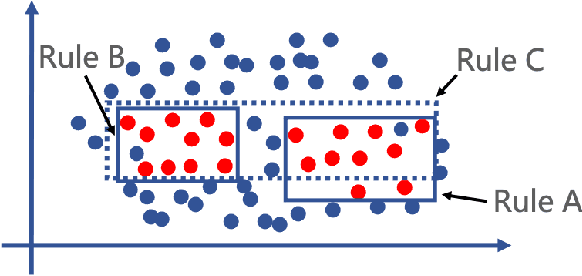
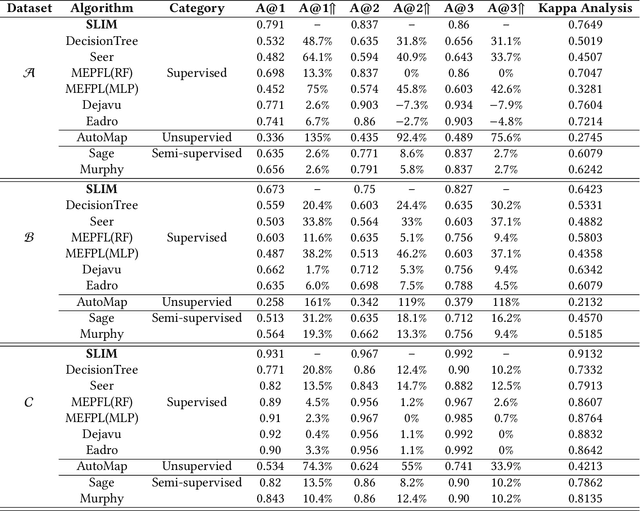
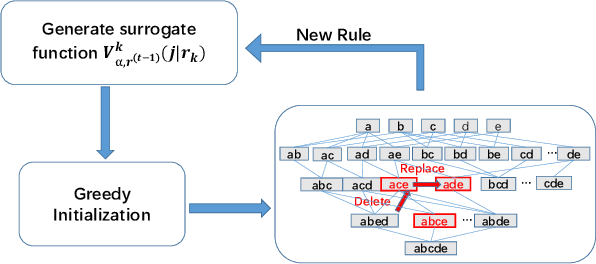
The newly deployed service -- one kind of change service, could lead to a new type of minority fault. Existing state-of-the-art methods for fault localization rarely consider the imbalanced fault classification in change service. This paper proposes a novel method that utilizes decision rule sets to deal with highly imbalanced data by optimizing the F1 score subject to cardinality constraints. The proposed method greedily generates the rule with maximal marginal gain and uses an efficient minorize-maximization (MM) approach to select rules iteratively, maximizing a non-monotone submodular lower bound. Compared with existing fault localization algorithms, our algorithm can adapt to the imbalanced fault scenario of change service, and provide interpretable fault causes which are easy to understand and verify. Our method can also be deployed in the online training setting, with only about 15% training overhead compared to the current SOTA methods. Empirical studies showcase that our algorithm outperforms existing fault localization algorithms in both accuracy and model interpretability.

Learning Interpretable Decision Rule Sets: A Submodular Optimization Approach

Rule sets are highly interpretable logical models in which the predicates for decision are expressed in disjunctive normal form (DNF, OR-of-ANDs), or, equivalently, the overall model comprises an unordered collection of if-then decision rules. In this paper, we consider a submodular optimization based approach for learning rule sets. The learning problem is framed as a subset selection task in which a subset of all possible rules needs to be selected to form an accurate and interpretable rule set. We employ an objective function that exhibits submodularity and thus is amenable to submodular optimization techniques. To overcome the difficulty arose from dealing with the exponential-sized ground set of rules, the subproblem of searching a rule is casted as another subset selection task that asks for a subset of features. We show it is possible to write the induced objective function for the subproblem as a difference of two submodular (DS) functions to make it approximately solvable by DS optimization algorithms. Overall, the proposed approach is simple, scalable, and likely to be benefited from further research on submodular optimization. Experiments on real datasets demonstrate the effectiveness of our method.