Deep-Learning Recognition of Scanning Transmission Electron Microscopy: Quantifying and Mitigating the Influence of Gaussian Noises

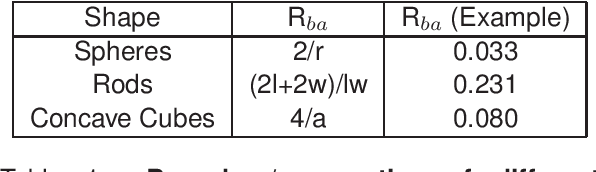
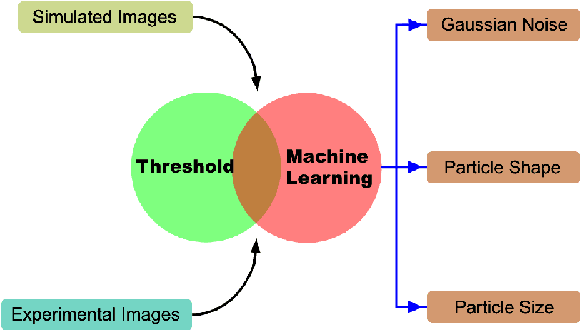
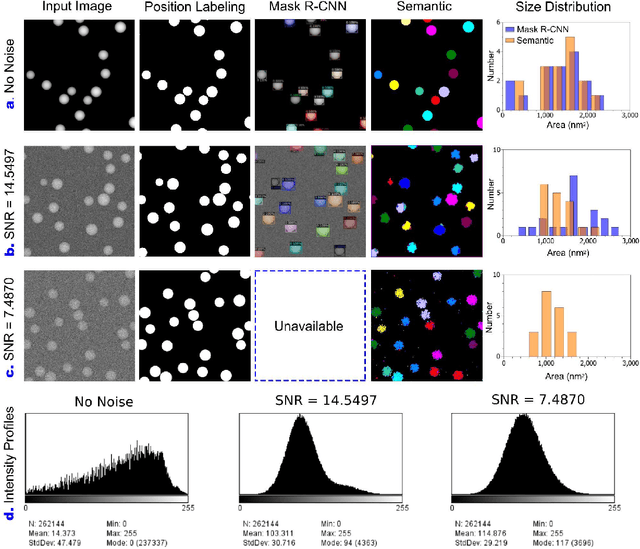
Scanning transmission electron microscopy (STEM) is a powerful tool to reveal the morphologies and structures of materials, thereby attracting intensive interests from the scientific and industrial communities. The outstanding spatial (atomic level) and temporal (ms level) resolutions of the STEM techniques generate fruitful amounts of high-definition data, thereby enabling the high-volume and high-speed analysis of materials. On the other hand, processing of the big dataset generated by STEM is time-consuming and beyond the capability of human-based manual work, which urgently calls for computer-based automation. In this work, we present a deep-learning mask region-based neural network (Mask R-CNN) for the recognition of nanoparticles imaged by STEM, as well as generating the associated dimensional analysis. The Mask R-CNN model was tested on simulated STEM-HAADF results with different Gaussian noises, particle shapes and particle sizes, and the results indicated that Gaussian noise has determining influence on the accuracy of recognition. By applying Gaussian and Non-Local Means filters on the noise-containing STEM-HAADF results, the influences of noises are largely mitigated, and recognition accuracy is significantly improved. This filtering-recognition approach was further applied to experimental STEM-HAADF results, which yields satisfying accuracy compared with the traditional threshold methods. The deep-learning-based method developed in this work has great potentials in analysis of the complicated structures and large data generated by STEM-HAADF.

Efficient Variational Inference for Sparse Deep Learning with Theoretical Guarantee

Sparse deep learning aims to address the challenge of huge storage consumption by deep neural networks, and to recover the sparse structure of target functions. Although tremendous empirical successes have been achieved, most sparse deep learning algorithms are lacking of theoretical support. On the other hand, another line of works have proposed theoretical frameworks that are computationally infeasible. In this paper, we train sparse deep neural networks with a fully Bayesian treatment under spike-and-slab priors, and develop a set of computationally efficient variational inferences via continuous relaxation of Bernoulli distribution. The variational posterior contraction rate is provided, which justifies the consistency of the proposed variational Bayes method. Notably, our empirical results demonstrate that this variational procedure provides uncertainty quantification in terms of Bayesian predictive distribution and is also capable to accomplish consistent variable selection by training a sparse multi-layer neural network.

Nearly Optimal Variational Inference for High Dimensional Regression with Shrinkage Priors

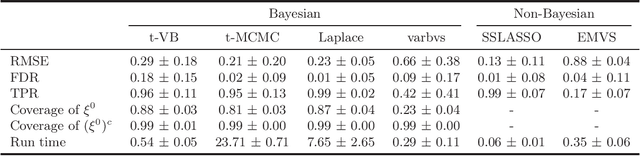
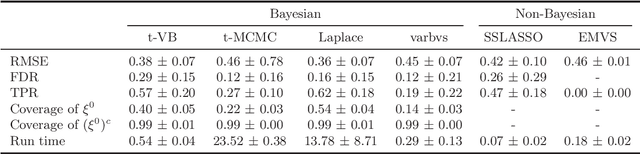
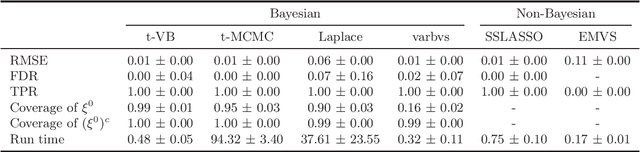
We propose a variational Bayesian (VB) procedure for high-dimensional linear model inferences with heavy tail shrinkage priors, such as student-t prior. Theoretically, we establish the consistency of the proposed VB method and prove that under the proper choice of prior specifications, the contraction rate of the VB posterior is nearly optimal. It justifies the validity of VB inference as an alternative of Markov Chain Monte Carlo (MCMC) sampling. Meanwhile, comparing to conventional MCMC methods, the VB procedure achieves much higher computational efficiency, which greatly alleviates the computing burden for modern machine learning applications such as massive data analysis. Through numerical studies, we demonstrate that the proposed VB method leads to shorter computing time, higher estimation accuracy, and lower variable selection error than competitive sparse Bayesian methods.

Stein Neural Sampler

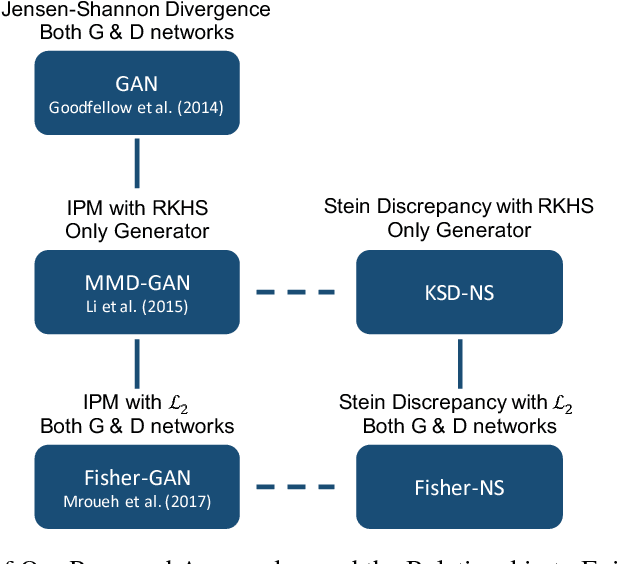
We propose two novel samplers to produce high-quality samples from a given (un-normalized) probability density. The sampling is achieved by transforming a reference distribution to the target distribution with neural networks, which are trained separately by minimizing two kinds of Stein Discrepancies, and hence our method is named as Stein neural sampler. Theoretical and empirical results suggest that, compared with traditional sampling schemes, our samplers share the following three advantages: 1. Being asymptotically correct; 2. Experiencing less convergence issue in practice; 3. Generating samples instantaneously.