JieZhang Cao
Joint Wasserstein Distribution Matching
Mar 01, 2020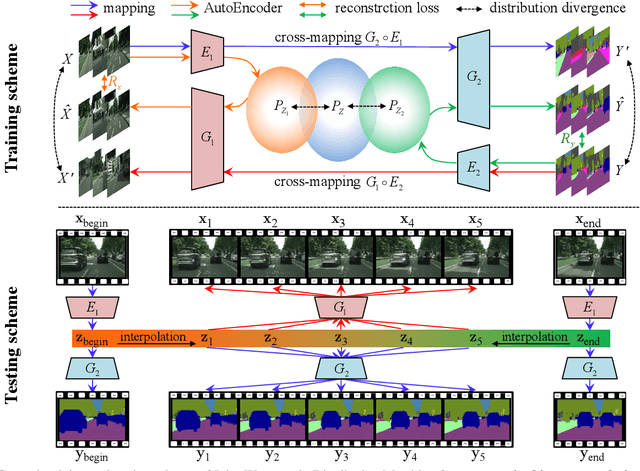

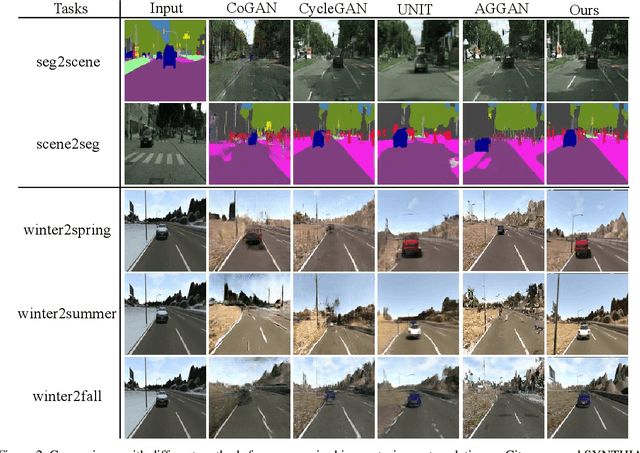

Abstract:Joint distribution matching (JDM) problem, which aims to learn bidirectional mappings to match joint distributions of two domains, occurs in many machine learning and computer vision applications. This problem, however, is very difficult due to two critical challenges: (i) it is often difficult to exploit sufficient information from the joint distribution to conduct the matching; (ii) this problem is hard to formulate and optimize. In this paper, relying on optimal transport theory, we propose to address JDM problem by minimizing the Wasserstein distance of the joint distributions in two domains. However, the resultant optimization problem is still intractable. We then propose an important theorem to reduce the intractable problem into a simple optimization problem, and develop a novel method (called Joint Wasserstein Distribution Matching (JWDM)) to solve it. In the experiments, we apply our method to unsupervised image translation and cross-domain video synthesis. Both qualitative and quantitative comparisons demonstrate the superior performance of our method over several state-of-the-arts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge