Adversarial Sleeping Bandit Problems with Multiple Plays: Algorithm and Ranking Application

This paper presents an efficient algorithm to solve the sleeping bandit with multiple plays problem in the context of an online recommendation system. The problem involves bounded, adversarial loss and unknown i.i.d. distributions for arm availability. The proposed algorithm extends the sleeping bandit algorithm for single arm selection and is guaranteed to achieve theoretical performance with regret upper bounded by $\bigO(kN^2\sqrt{T\log T})$, where $k$ is the number of arms selected per time step, $N$ is the total number of arms, and $T$ is the time horizon.

Online Convex Optimization with Long Term Constraints for Predictable Sequences

In this paper, we investigate the framework of Online Convex Optimization (OCO) for online learning. OCO offers a very powerful online learning framework for many applications. In this context, we study a specific framework of OCO called {\it OCO with long term constraints}. Long term constraints are introduced typically as an alternative to reduce the complexity of the projection at every update step in online optimization. While many algorithmic advances have been made towards online optimization with long term constraints, these algorithms typically assume that the sequence of cost functions over a certain $T$ finite steps that determine the cost to the online learner are adversarially generated. In many circumstances, the sequence of cost functions may not be unrelated, and thus predictable from those observed till a point of time. In this paper, we study the setting where the sequences are predictable. We present a novel online optimization algorithm for online optimization with long term constraints that can leverage such predictability. We show that, with a predictor that can supply the gradient information of the next function in the sequence, our algorithm can achieve an overall regret and constraint violation rate that is strictly less than the rate that is achievable without prediction.

Online Learning for Receding Horizon Control with Provable Regret Guarantees

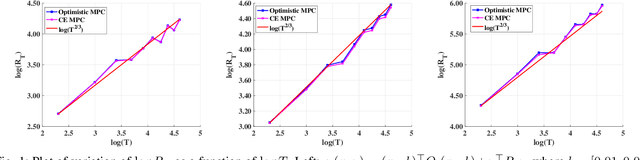
We address the problem of learning to control an unknown linear dynamical system with time varying cost functions through the framework of online Receding Horizon Control (RHC). We consider the setting where the control algorithm does not know the true system model and has only access to a fixed-length (that does not grow with the control horizon) preview of the future cost functions. We characterize the performance of an algorithm using the metric of dynamic regret, which is defined as the difference between the cumulative cost incurred by the algorithm and that of the best sequence of actions in hindsight. We propose two different online RHC algorithms to address this problem, namely Certainty Equivalence RHC (CE-RHC) algorithm and Optimistic RHC (O-RHC) algorithm. We show that under the standard stability assumption for the model estimate, the CE-RHC algorithm achieves $\mathcal{O}(T^{2/3})$ dynamic regret. We then extend this result to the setting where the stability assumption hold only for the true system model by proposing the O-RHC algorithm. We show that O-RHC algorithm achieves $\mathcal{O}(T^{2/3})$ dynamic regret but with some additional computation.

Online Convex Optimization in Changing Environments and its Application to Resource Allocation

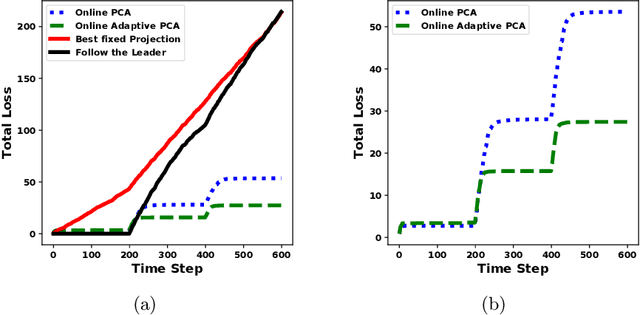
In the era of the big data, we create and collect lots of data from all different kinds of sources: the Internet, the sensors, the consumer market, and so on. Many of the data are coming sequentially, and would like to be processed and understood quickly. One classic way of analyzing data is based on batch processing, in which the data is stored and analyzed in an offline fashion. However, when the volume of the data is too large, it is much more difficult and time-consuming to do batch processing than sequential processing. What's more, sequential data is usually changing dynamically, and needs to be understood on-the-fly in order to capture the changes. Online Convex Optimization (OCO) is a popular framework that matches the above sequential data processing requirement. Applications using OCO include online routing, online auctions, online classification and regression, as well as online resource allocation. Due to the general applicability of OCO to the sequential data and the rigorous theoretical guarantee, it has attracted lots of researchers to develop useful algorithms to fulfill different needs. In this thesis, we show our contributions to OCO's development by designing algorithms to adapt to changing environments.

Trading-Off Static and Dynamic Regret in Online Least-Squares and Beyond

Recursive least-squares algorithms often use forgetting factors as a heuristic to adapt to non-stationary data streams. % The first contribution of this paper rigorously characterizes the effect of forgetting factors for a class of online Newton algorithms. % For exp-concave and strongly convex objectives, the algorithms achieve a dynamic regret of $\max\{O(\log T),O(\sqrt{TV})\}$, where $V$ is a bound on the path length of the comparison sequence. % In particular, we show how classic recursive least-squares with a forgetting factor achieves this dynamic regret bound. % By varying $V$, we obtain a trade-off between static and dynamic regret. % Furthermore, we show how the forgetting factor can be tuned to obtain % trade-offs between static and dynamic regret. % In order to obtain more computationally efficient algorithms, our second contribution is a novel gradient descent step size rule for strongly convex functions. % Our gradient descent rule recovers the dynamic regret bounds described above. % For smooth problems, we can also obtain static regret of $O(T^{1-\beta})$ and dynamic regret of $O(T^\beta V^*)$, where $\beta \in (0,1)$ and $V^*$ is the path length of the sequence of minimizers. % By varying $\beta$, we obtain a trade-off between static and dynamic regret.

Online Adaptive Principal Component Analysis and Its extensions

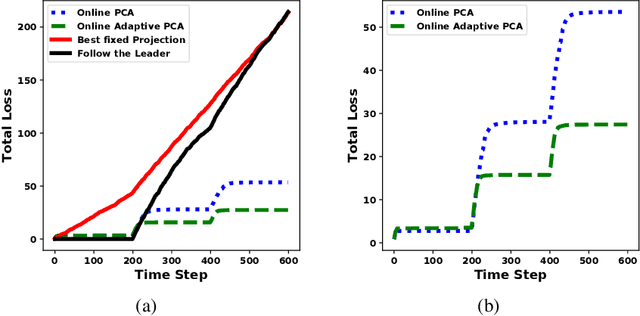
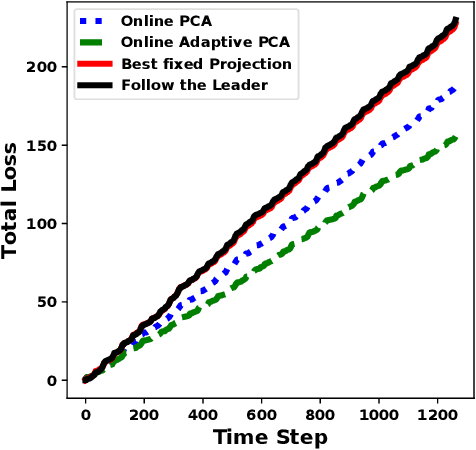
We propose algorithms for online principal component analysis (PCA) and variance minimization for adaptive settings. Previous literature has focused on upper bounding the static adversarial regret, whose comparator is the optimal fixed action in hindsight. However, static regret is not an appropriate metric when the underlying environment is changing. Instead, we adopt the adaptive regret metric from the previous literature and propose online adaptive algorithms for PCA and variance minimization, that have sub-linear adaptive regret guarantees. We demonstrate both theoretically and experimentally that the proposed algorithms can adapt to the changing environments.

Online Convex Optimization for Cumulative Constraints

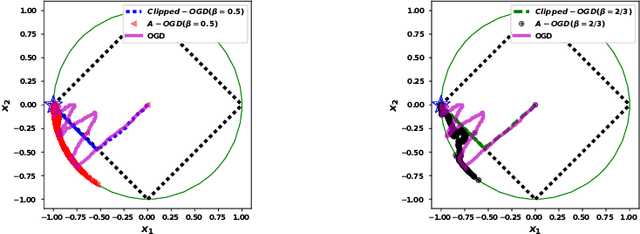
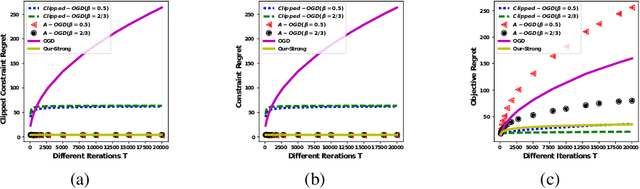
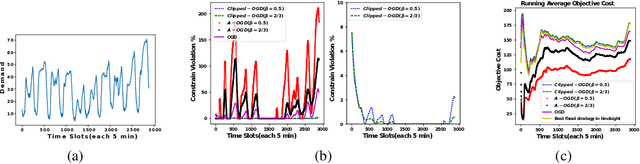
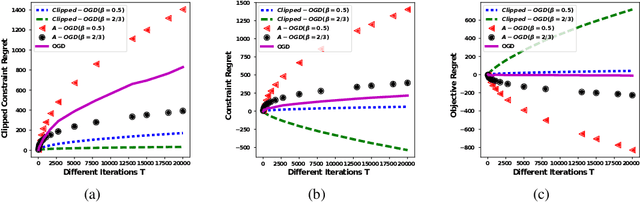
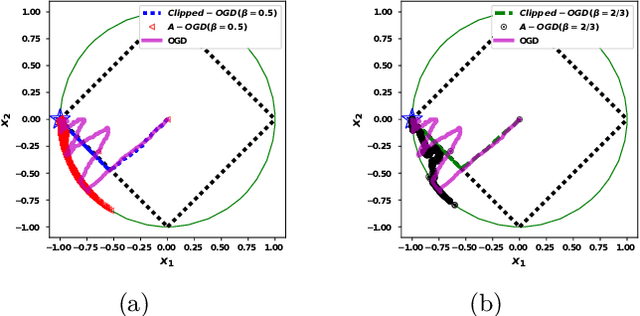
We propose the algorithms for online convex optimization which lead to cumulative squared constraint violations of the form $\sum\limits_{t=1}^T\big([g(x_t)]_+\big)^2=O(T^{1-\beta})$, where $\beta\in(0,1)$. Previous literature has focused on long-term constraints of the form $\sum\limits_{t=1}^Tg(x_t)$. There, strictly feasible solutions can cancel out the effects of violated constraints. In contrast, the new form heavily penalizes large constraint violations and cancellation effects cannot occur. Furthermore, useful bounds on the single step constraint violation $[g(x_t)]_+$ are derived. For convex objectives, our regret bounds generalize existing bounds, and for strongly convex objectives we give improved regret bounds. In numerical experiments, we show that our algorithm closely follows the constraint boundary leading to low cumulative violation.