Function Gradient Approximation with Random Shallow ReLU Networks with Control Applications

Neural networks are widely used to approximate unknown functions in control. A common neural network architecture uses a single hidden layer (i.e. a shallow network), in which the input parameters are fixed in advance and only the output parameters are trained. The typical formal analysis asserts that if output parameters exist to approximate the unknown function with sufficient accuracy, then desired control performance can be achieved. A long-standing theoretical gap was that no conditions existed to guarantee that, for the fixed input parameters, required accuracy could be obtained by training the output parameters. Our recent work has partially closed this gap by demonstrating that if input parameters are chosen randomly, then for any sufficiently smooth function, with high-probability there are output parameters resulting in $O((1/m)^{1/2})$ approximation errors, where $m$ is the number of neurons. However, some applications, notably continuous-time value function approximation, require that the network approximates the both the unknown function and its gradient with sufficient accuracy. In this paper, we show that randomly generated input parameters and trained output parameters result in gradient errors of $O((\log(m)/m)^{1/2})$, and additionally, improve the constants from our prior work. We show how to apply the result to policy evaluation problems.

Approximation with Random Shallow ReLU Networks with Applications to Model Reference Adaptive Control

Neural networks are regularly employed in adaptive control of nonlinear systems and related methods o reinforcement learning. A common architecture uses a neural network with a single hidden layer (i.e. a shallow network), in which the weights and biases are fixed in advance and only the output layer is trained. While classical results show that there exist neural networks of this type that can approximate arbitrary continuous functions over bounded regions, they are non-constructive, and the networks used in practice have no approximation guarantees. Thus, the approximation properties required for control with neural networks are assumed, rather than proved. In this paper, we aim to fill this gap by showing that for sufficiently smooth functions, ReLU networks with randomly generated weights and biases achieve $L_{\infty}$ error of $O(m^{-1/2})$ with high probability, where $m$ is the number of neurons. It suffices to generate the weights uniformly over a sphere and the biases uniformly over an interval. We show how the result can be used to get approximations of required accuracy in a model reference adaptive control application.

Function Approximation with Randomly Initialized Neural Networks for Approximate Model Reference Adaptive Control

Classical results in neural network approximation theory show how arbitrary continuous functions can be approximated by networks with a single hidden layer, under mild assumptions on the activation function. However, the classical theory does not give a constructive means to generate the network parameters that achieve a desired accuracy. Recent results have demonstrated that for specialized activation functions, such as ReLUs and some classes of analytic functions, high accuracy can be achieved via linear combinations of randomly initialized activations. These recent works utilize specialized integral representations of target functions that depend on the specific activation functions used. This paper defines mollified integral representations, which provide a means to form integral representations of target functions using activations for which no direct integral representation is currently known. The new construction enables approximation guarantees for randomly initialized networks for a variety of widely used activation functions.

Non-Asymptotic Pointwise and Worst-Case Bounds for Classical Spectrum Estimators

Spectrum estimation is a fundamental methodology in the analysis of time-series data, with applications including medicine, speech analysis, and control design. The asymptotic theory of spectrum estimation is well-understood, but the theory is limited when the number of samples is fixed and finite. This paper gives non-asymptotic error bounds for a broad class of spectral estimators, both pointwise (at specific frequencies) and in the worst case over all frequencies. The general method is used to derive error bounds for the classical Blackman-Tukey, Bartlett, and Welch estimators.

Constrained Langevin Algorithms with L-mixing External Random Variables

Langevin algorithms are gradient descent methods augmented with additive noise, and are widely used in Markov Chain Monte Carlo (MCMC) sampling, optimization, and learning. In recent years, the non-asymptotic analysis of Langevin algorithms for non-convex optimization learning has been extensively explored. For constrained problems with non-convex losses over compact convex domain in the case of IID data variables, Langevin algorithm achieves a deviation of $O(T^{-1/4} (\log T)^{1/2})$ from its target distribution [22]. In this paper, we obtain a deviation of $O(T^{-1/2} \log T)$ in $1$-Wasserstein distance for non-convex losses with $L$-mixing data variables and polyhedral constraints (which are not necessarily bounded). This deviation indicates that our convergence rate is faster than those in the previous works on constrained Langevin algorithms for non-convex optimization.

Projected Stochastic Gradient Langevin Algorithms for Constrained Sampling and Non-Convex Learning

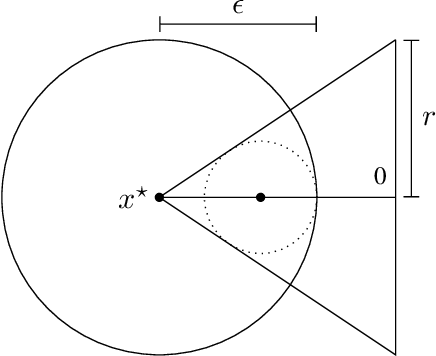
Langevin algorithms are gradient descent methods with additive noise. They have been used for decades in Markov chain Monte Carlo (MCMC) sampling, optimization, and learning. Their convergence properties for unconstrained non-convex optimization and learning problems have been studied widely in the last few years. Other work has examined projected Langevin algorithms for sampling from log-concave distributions restricted to convex compact sets. For learning and optimization, log-concave distributions correspond to convex losses. In this paper, we analyze the case of non-convex losses with compact convex constraint sets and IID external data variables. We term the resulting method the projected stochastic gradient Langevin algorithm (PSGLA). We show the algorithm achieves a deviation of $O(T^{-1/4}(\log T)^{1/2})$ from its target distribution in 1-Wasserstein distance. For optimization and learning, we show that the algorithm achieves $\epsilon$-suboptimal solutions, on average, provided that it is run for a time that is polynomial in $\epsilon^{-1}$ and slightly super-exponential in the problem dimension.

Trading-Off Static and Dynamic Regret in Online Least-Squares and Beyond

Recursive least-squares algorithms often use forgetting factors as a heuristic to adapt to non-stationary data streams. % The first contribution of this paper rigorously characterizes the effect of forgetting factors for a class of online Newton algorithms. % For exp-concave and strongly convex objectives, the algorithms achieve a dynamic regret of $\max\{O(\log T),O(\sqrt{TV})\}$, where $V$ is a bound on the path length of the comparison sequence. % In particular, we show how classic recursive least-squares with a forgetting factor achieves this dynamic regret bound. % By varying $V$, we obtain a trade-off between static and dynamic regret. % Furthermore, we show how the forgetting factor can be tuned to obtain % trade-offs between static and dynamic regret. % In order to obtain more computationally efficient algorithms, our second contribution is a novel gradient descent step size rule for strongly convex functions. % Our gradient descent rule recovers the dynamic regret bounds described above. % For smooth problems, we can also obtain static regret of $O(T^{1-\beta})$ and dynamic regret of $O(T^\beta V^*)$, where $\beta \in (0,1)$ and $V^*$ is the path length of the sequence of minimizers. % By varying $\beta$, we obtain a trade-off between static and dynamic regret.

Simple Algorithms for Dueling Bandits

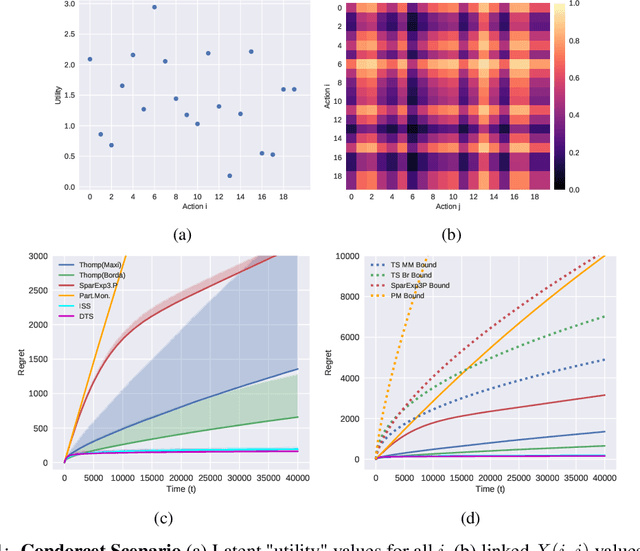
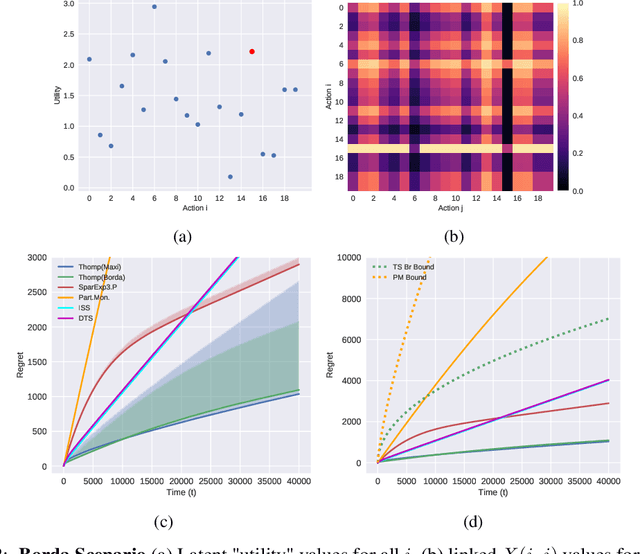
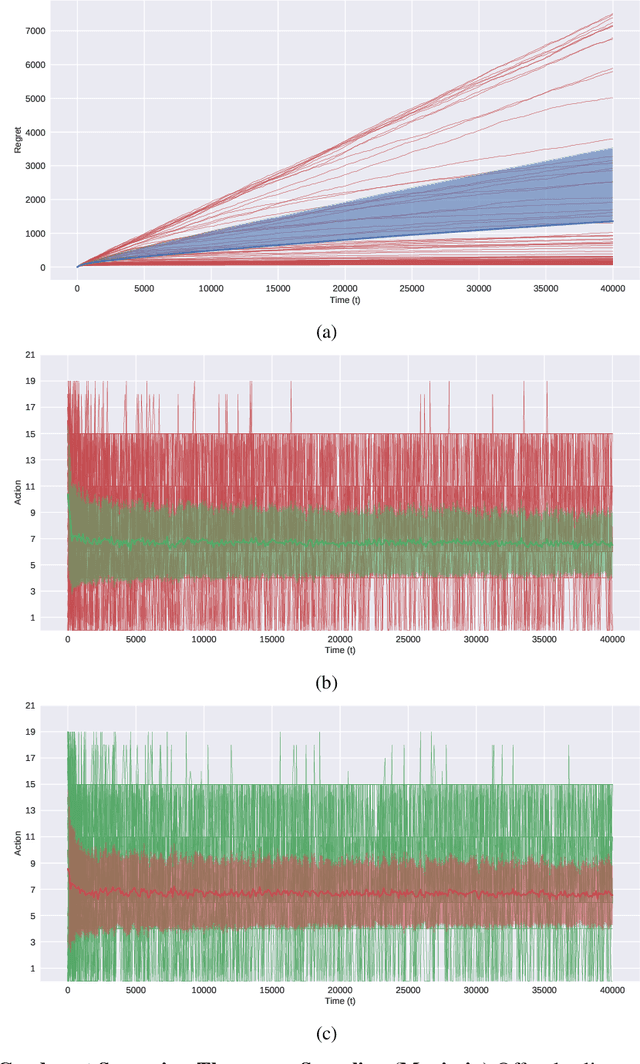
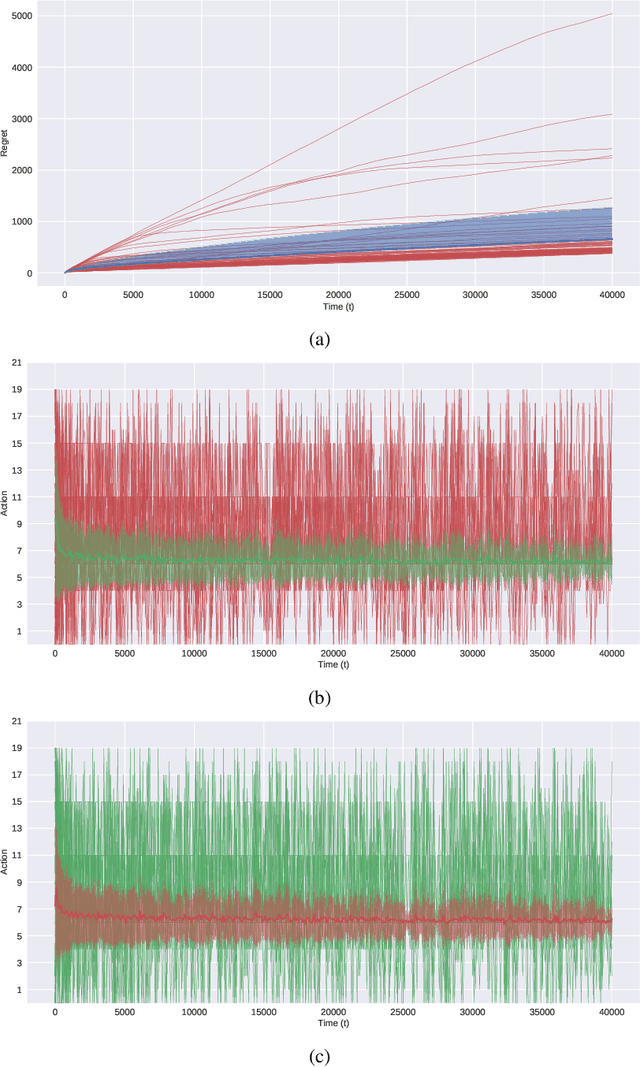
In this paper, we present simple algorithms for Dueling Bandits. We prove that the algorithms have regret bounds for time horizon T of order O(T^rho ) with 1/2 <= rho <= 3/4, which importantly do not depend on any preference gap between actions, Delta. Dueling Bandits is an important extension of the Multi-Armed Bandit problem, in which the algorithm must select two actions at a time and only receives binary feedback for the duel outcome. This is analogous to comparisons in which the rater can only provide yes/no or better/worse type responses. We compare our simple algorithms to the current state-of-the-art for Dueling Bandits, ISS and DTS, discussing complexity and regret upper bounds, and conducting experiments on synthetic data that demonstrate their regret performance, which in some cases exceeds state-of-the-art.

Online Adaptive Principal Component Analysis and Its extensions

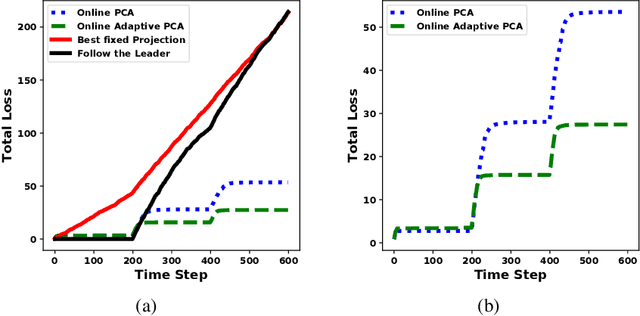
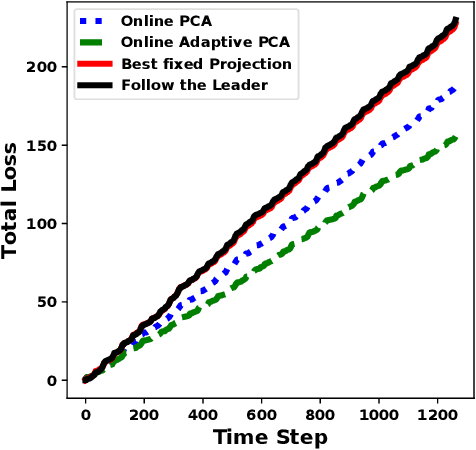
We propose algorithms for online principal component analysis (PCA) and variance minimization for adaptive settings. Previous literature has focused on upper bounding the static adversarial regret, whose comparator is the optimal fixed action in hindsight. However, static regret is not an appropriate metric when the underlying environment is changing. Instead, we adopt the adaptive regret metric from the previous literature and propose online adaptive algorithms for PCA and variance minimization, that have sub-linear adaptive regret guarantees. We demonstrate both theoretically and experimentally that the proposed algorithms can adapt to the changing environments.

Online Convex Optimization for Cumulative Constraints

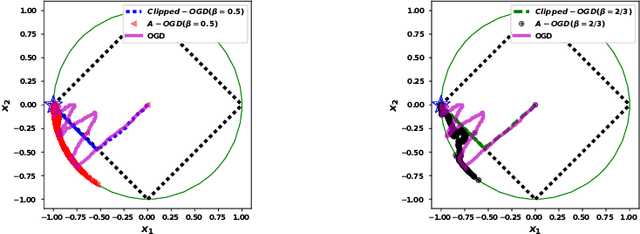
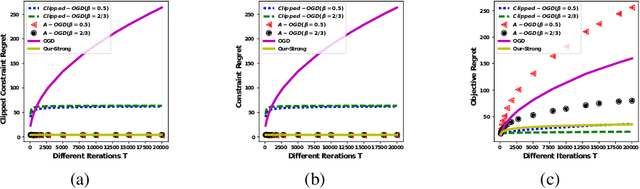
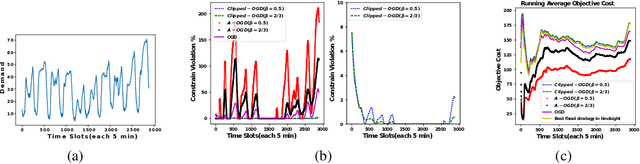
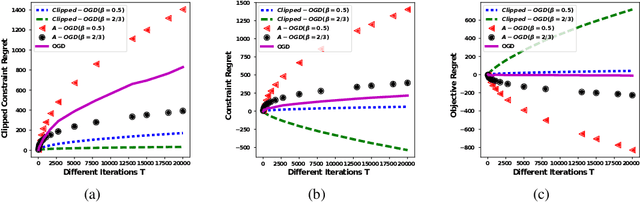
We propose the algorithms for online convex optimization which lead to cumulative squared constraint violations of the form $\sum\limits_{t=1}^T\big([g(x_t)]_+\big)^2=O(T^{1-\beta})$, where $\beta\in(0,1)$. Previous literature has focused on long-term constraints of the form $\sum\limits_{t=1}^Tg(x_t)$. There, strictly feasible solutions can cancel out the effects of violated constraints. In contrast, the new form heavily penalizes large constraint violations and cancellation effects cannot occur. Furthermore, useful bounds on the single step constraint violation $[g(x_t)]_+$ are derived. For convex objectives, our regret bounds generalize existing bounds, and for strongly convex objectives we give improved regret bounds. In numerical experiments, we show that our algorithm closely follows the constraint boundary leading to low cumulative violation.