Simple Algorithms for Dueling Bandits
Paper and Code
Jun 18, 2019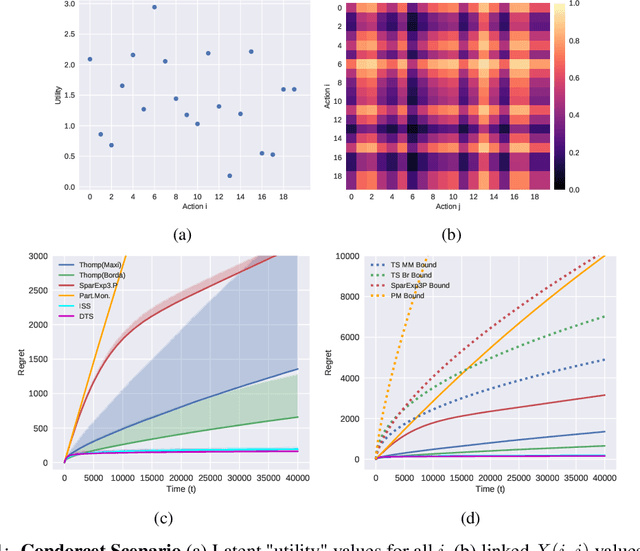
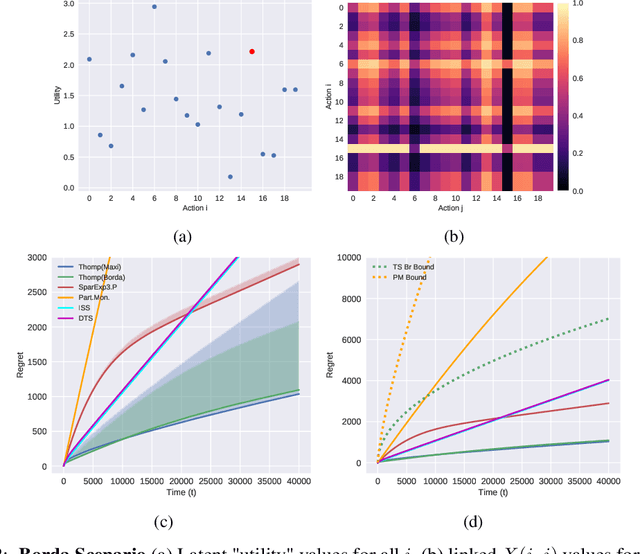
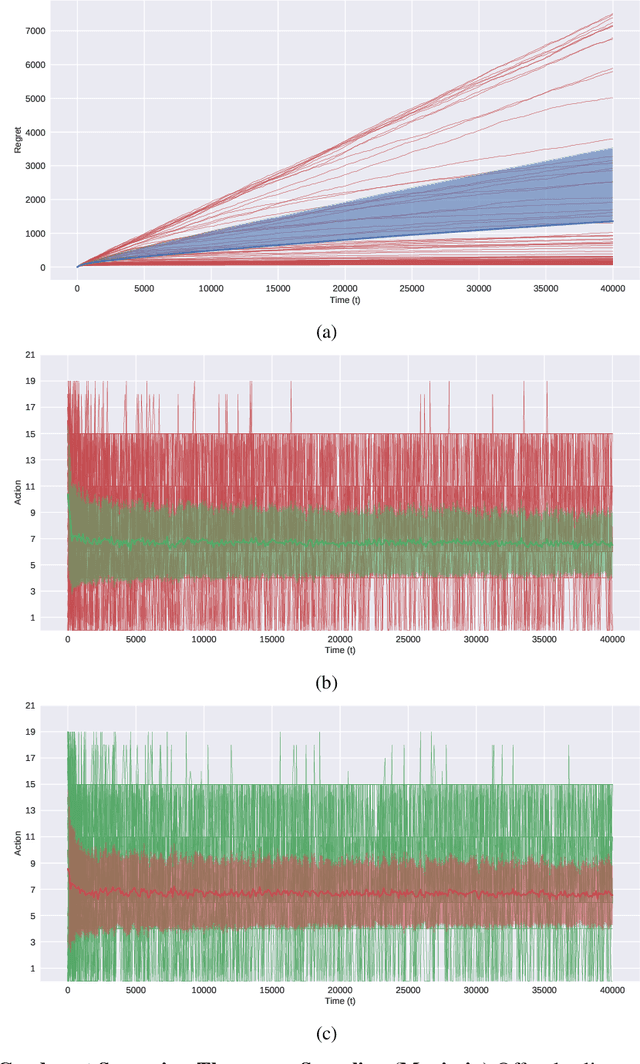
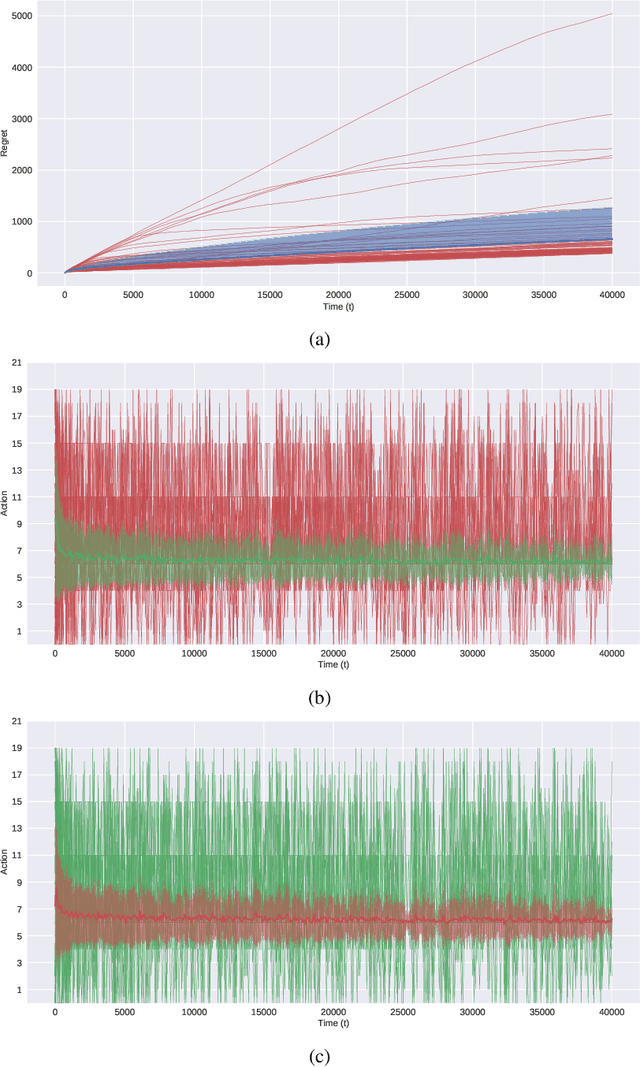
In this paper, we present simple algorithms for Dueling Bandits. We prove that the algorithms have regret bounds for time horizon T of order O(T^rho ) with 1/2 <= rho <= 3/4, which importantly do not depend on any preference gap between actions, Delta. Dueling Bandits is an important extension of the Multi-Armed Bandit problem, in which the algorithm must select two actions at a time and only receives binary feedback for the duel outcome. This is analogous to comparisons in which the rater can only provide yes/no or better/worse type responses. We compare our simple algorithms to the current state-of-the-art for Dueling Bandits, ISS and DTS, discussing complexity and regret upper bounds, and conducting experiments on synthetic data that demonstrate their regret performance, which in some cases exceeds state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge