Approximation with Random Shallow ReLU Networks with Applications to Model Reference Adaptive Control

Neural networks are regularly employed in adaptive control of nonlinear systems and related methods o reinforcement learning. A common architecture uses a neural network with a single hidden layer (i.e. a shallow network), in which the weights and biases are fixed in advance and only the output layer is trained. While classical results show that there exist neural networks of this type that can approximate arbitrary continuous functions over bounded regions, they are non-constructive, and the networks used in practice have no approximation guarantees. Thus, the approximation properties required for control with neural networks are assumed, rather than proved. In this paper, we aim to fill this gap by showing that for sufficiently smooth functions, ReLU networks with randomly generated weights and biases achieve $L_{\infty}$ error of $O(m^{-1/2})$ with high probability, where $m$ is the number of neurons. It suffices to generate the weights uniformly over a sphere and the biases uniformly over an interval. We show how the result can be used to get approximations of required accuracy in a model reference adaptive control application.

Function Approximation with Randomly Initialized Neural Networks for Approximate Model Reference Adaptive Control

Classical results in neural network approximation theory show how arbitrary continuous functions can be approximated by networks with a single hidden layer, under mild assumptions on the activation function. However, the classical theory does not give a constructive means to generate the network parameters that achieve a desired accuracy. Recent results have demonstrated that for specialized activation functions, such as ReLUs and some classes of analytic functions, high accuracy can be achieved via linear combinations of randomly initialized activations. These recent works utilize specialized integral representations of target functions that depend on the specific activation functions used. This paper defines mollified integral representations, which provide a means to form integral representations of target functions using activations for which no direct integral representation is currently known. The new construction enables approximation guarantees for randomly initialized networks for a variety of widely used activation functions.

Simple Algorithms for Dueling Bandits

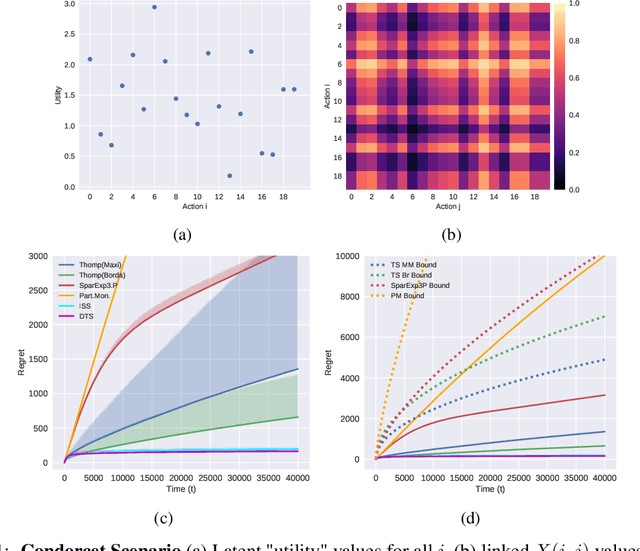
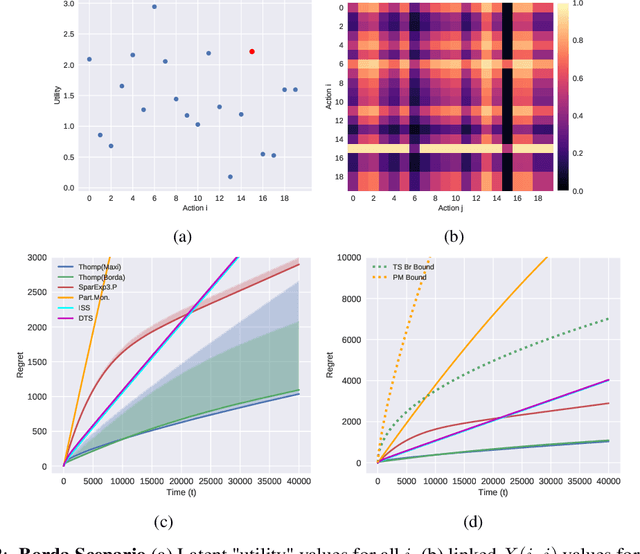
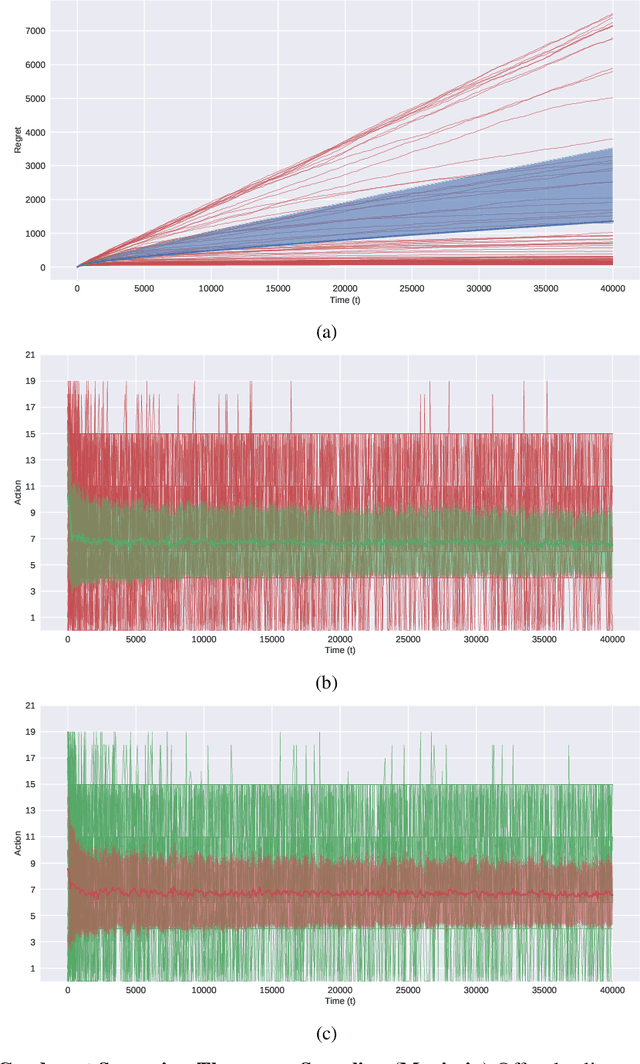
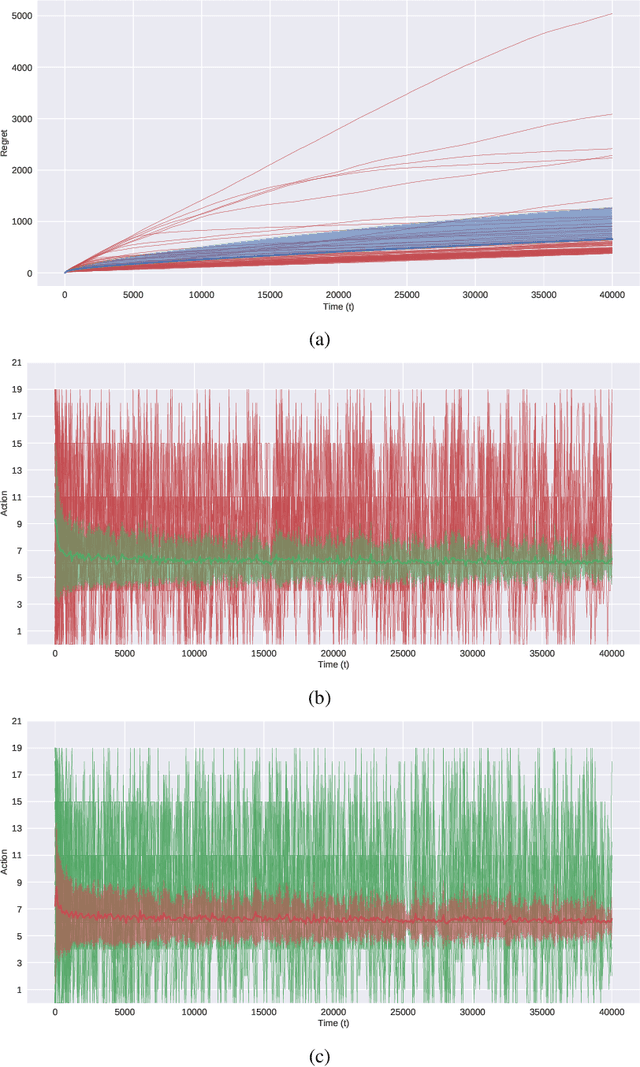
In this paper, we present simple algorithms for Dueling Bandits. We prove that the algorithms have regret bounds for time horizon T of order O(T^rho ) with 1/2 <= rho <= 3/4, which importantly do not depend on any preference gap between actions, Delta. Dueling Bandits is an important extension of the Multi-Armed Bandit problem, in which the algorithm must select two actions at a time and only receives binary feedback for the duel outcome. This is analogous to comparisons in which the rater can only provide yes/no or better/worse type responses. We compare our simple algorithms to the current state-of-the-art for Dueling Bandits, ISS and DTS, discussing complexity and regret upper bounds, and conducting experiments on synthetic data that demonstrate their regret performance, which in some cases exceeds state-of-the-art.