Online Adaptive Principal Component Analysis and Its extensions
Paper and Code
Jan 23, 2019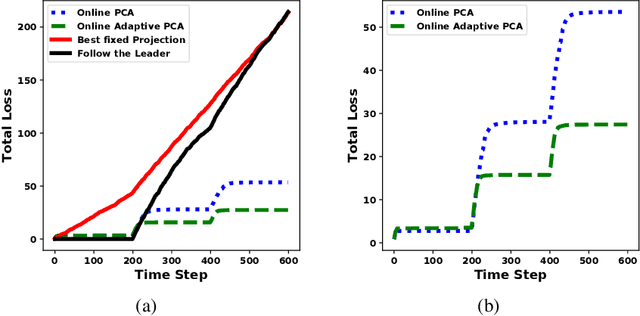
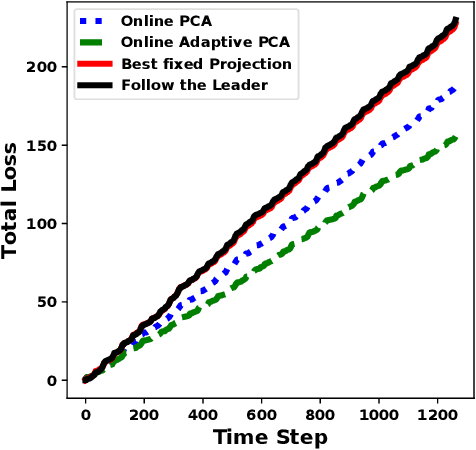
We propose algorithms for online principal component analysis (PCA) and variance minimization for adaptive settings. Previous literature has focused on upper bounding the static adversarial regret, whose comparator is the optimal fixed action in hindsight. However, static regret is not an appropriate metric when the underlying environment is changing. Instead, we adopt the adaptive regret metric from the previous literature and propose online adaptive algorithms for PCA and variance minimization, that have sub-linear adaptive regret guarantees. We demonstrate both theoretically and experimentally that the proposed algorithms can adapt to the changing environments.
* This paper is under review
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge