Online Learning for Receding Horizon Control with Provable Regret Guarantees

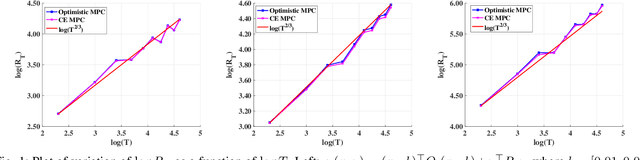
We address the problem of learning to control an unknown linear dynamical system with time varying cost functions through the framework of online Receding Horizon Control (RHC). We consider the setting where the control algorithm does not know the true system model and has only access to a fixed-length (that does not grow with the control horizon) preview of the future cost functions. We characterize the performance of an algorithm using the metric of dynamic regret, which is defined as the difference between the cumulative cost incurred by the algorithm and that of the best sequence of actions in hindsight. We propose two different online RHC algorithms to address this problem, namely Certainty Equivalence RHC (CE-RHC) algorithm and Optimistic RHC (O-RHC) algorithm. We show that under the standard stability assumption for the model estimate, the CE-RHC algorithm achieves $\mathcal{O}(T^{2/3})$ dynamic regret. We then extend this result to the setting where the stability assumption hold only for the true system model by proposing the O-RHC algorithm. We show that O-RHC algorithm achieves $\mathcal{O}(T^{2/3})$ dynamic regret but with some additional computation.