Jianfeng Du
A Noise-tolerant Differentiable Learning Approach for Single Occurrence Regular Expression with Interleaving
Dec 02, 2022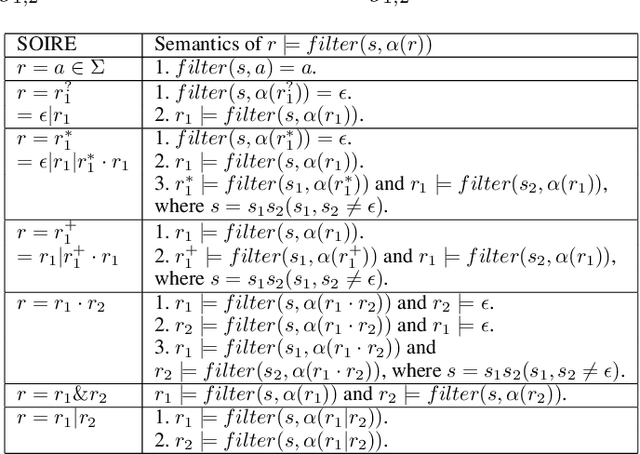
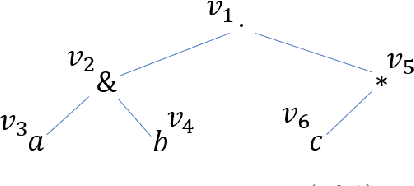
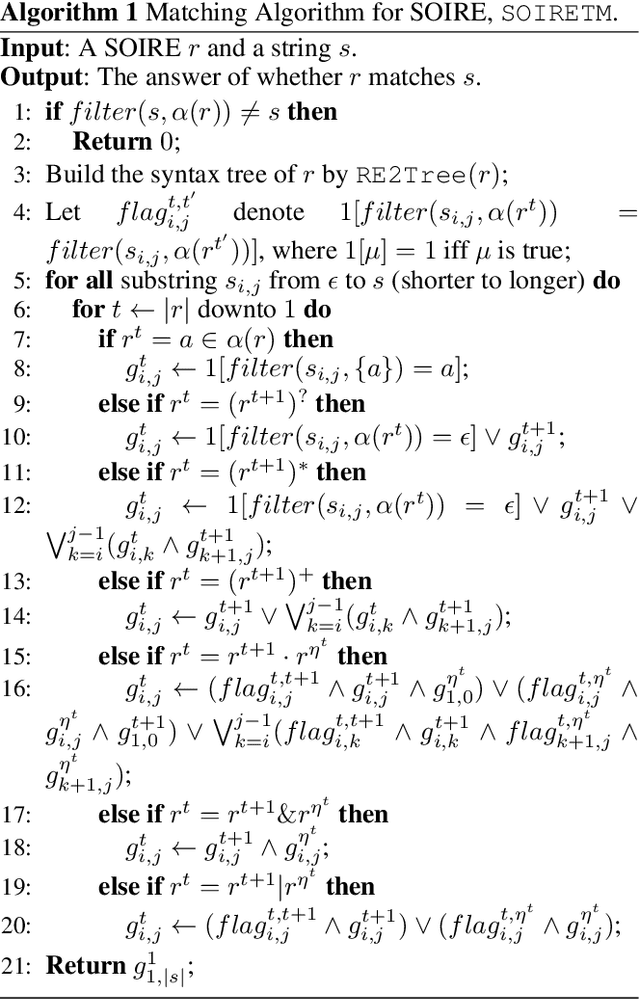
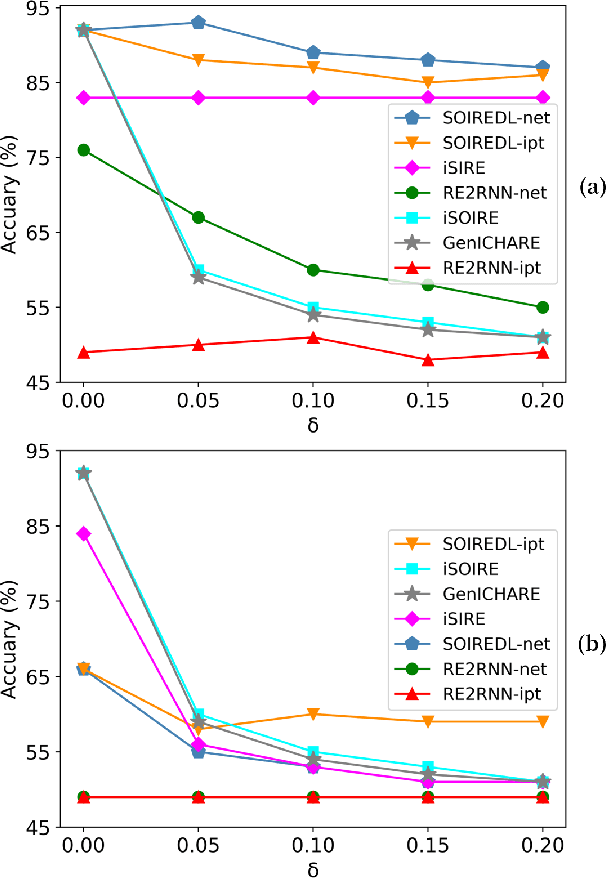
Abstract:We study the problem of learning a single occurrence regular expression with interleaving (SOIRE) from a set of text strings possibly with noise. SOIRE fully supports interleaving and covers a large portion of regular expressions used in practice. Learning SOIREs is challenging because it requires heavy computation and text strings usually contain noise in practice. Most of the previous studies only learn restricted SOIREs and are not robust on noisy data. To tackle these issues, we propose a noise-tolerant differentiable learning approach SOIREDL for SOIRE. We design a neural network to simulate SOIRE matching and theoretically prove that certain assignments of the set of parameters learnt by the neural network, called faithful encodings, are one-to-one corresponding to SOIREs for a bounded size. Based on this correspondence, we interpret the target SOIRE from an assignment of the set of parameters of the neural network by exploring the nearest faithful encodings. Experimental results show that SOIREDL outperforms the state-of-the-art approaches, especially on noisy data.
Merging Knowledge Bases in Possibilistic Logic by Lexicographic Aggregation
Mar 15, 2012
Abstract:Belief merging is an important but difficult problem in Artificial Intelligence, especially when sources of information are pervaded with uncertainty. Many merging operators have been proposed to deal with this problem in possibilistic logic, a weighted logic which is powerful for handling inconsistency and deal- ing with uncertainty. They often result in a possibilistic knowledge base which is a set of weighted formulas. Although possibilistic logic is inconsistency tolerant, it suers from the well-known "drowning effect". Therefore, we may still want to obtain a consistent possi- bilistic knowledge base as the result of merg- ing. In such a case, we argue that it is not always necessary to keep weighted informa- tion after merging. In this paper, we define a merging operator that maps a set of pos- sibilistic knowledge bases and a formula rep- resenting the integrity constraints to a clas- sical knowledge base by using lexicographic ordering. We show that it satisfies nine pos- tulates that generalize basic postulates for propositional merging given in [11]. These postulates capture the principle of minimal change in some sense. We then provide an algorithm for generating the resulting knowl- edge base of our merging operator. Finally, we discuss the compatibility of our merging operator with propositional merging and es- tablish the advantage of our merging opera- tor over existing semantic merging operators in the propositional case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge