RES - a Relative Method for Evidential Reasoning

In this paper we describe a novel method for evidential reasoning [1]. It involves modelling the process of evidential reasoning in three steps, namely, evidence structure construction, evidence accumulation, and decision making. The proposed method, called RES, is novel in that evidence strength is associated with an evidential support relationship (an argument) between a pair of statements and such strength is carried by comparison between arguments. This is in contrast to the onventional approaches, where evidence strength is represented numerically and is associated with a statement.

Discounting and Combination Operations in Evidential Reasoning

Evidential reasoning is now a leading topic in Artificial Intelligence. Evidence is represented by a variety of evidential functions. Evidential reasoning is carried out by certain kinds of fundamental operation on these functions. This paper discusses two of the basic operations on evidential functions, the discount operation and the well-known orthogonal sum operation. We show that the discount operation is not commutative with the orthogonal sum operation, and derive expressions for the two operations applied to the various evidential function.

Corporate Evidential Decision Making in Performance Prediction Domains

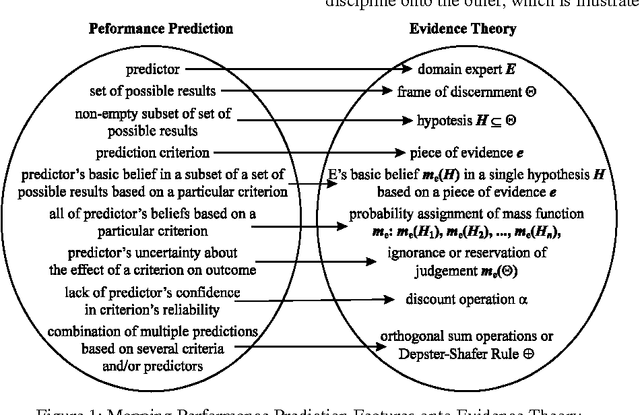
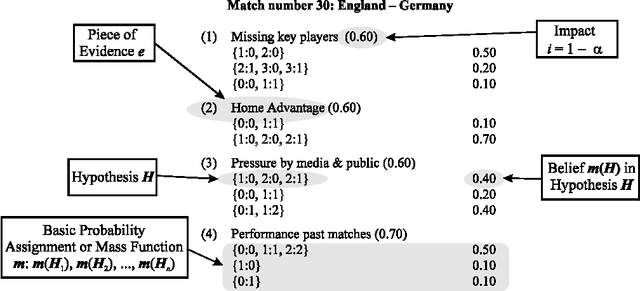
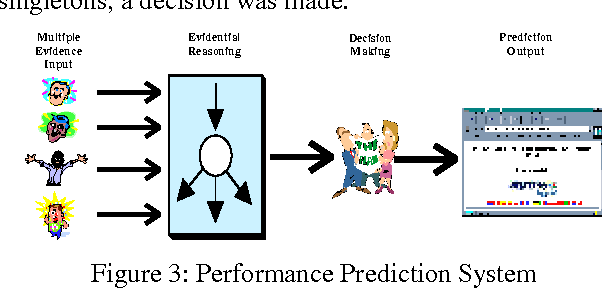
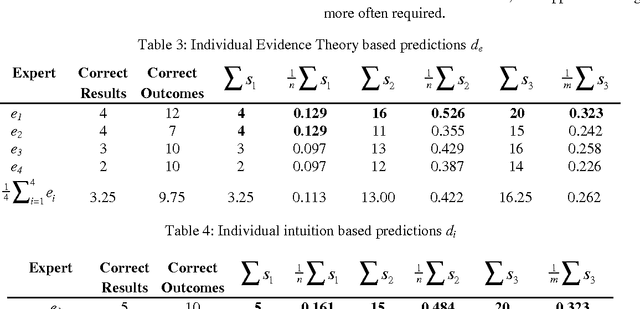
Performance prediction or forecasting sporting outcomes involves a great deal of insight into the particular area one is dealing with, and a considerable amount of intuition about the factors that bear on such outcomes and performances. The mathematical Theory of Evidence offers representation formalisms which grant experts a high degree of freedom when expressing their subjective beliefs in the context of decision-making situations like performance prediction. Furthermore, this reasoning framework incorporates a powerful mechanism to systematically pool the decisions made by individual subject matter experts. The idea behind such a combination of knowledge is to improve the competence (quality) of the overall decision-making process. This paper reports on a performance prediction experiment carried out during the European Football Championship in 1996. Relying on the knowledge of four predictors, Evidence Theory was used to forecast the final scores of all 31 matches. The results of this empirical study are very encouraging.

A Revision-Based Approach to Resolving Conflicting Information

In this paper, we propose a revision-based approach for conflict resolution by generalizing the Disjunctive Maxi-Adjustment (DMA) approach (Benferhat et al. 2004). Revision operators can be classified into two different families: the model-based ones and the formula-based ones. So the revision-based approach has two different versions according to which family of revision operators is chosen. Two particular revision operators are considered, one is the Dalal's revision operator, which is a model-based revision operator, and the other is the cardinality-maximal based revision operator, which is a formulabased revision operator. When the Dalal's revision operator is chosen, the revision-based approach is independent of the syntactic form in each stratum and it captures some notion of minimal change. When the cardinalitymaximal based revision operator is chosen, the revision-based approach is equivalent to the DMA approach. We also show that both approaches are computationally easier than the DMA approach.

Merging Knowledge Bases in Possibilistic Logic by Lexicographic Aggregation

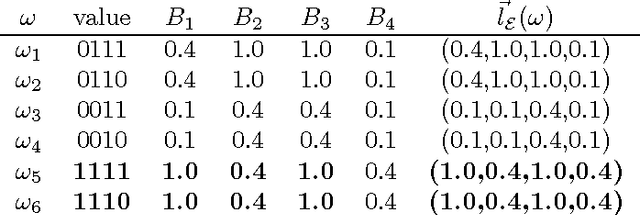
Belief merging is an important but difficult problem in Artificial Intelligence, especially when sources of information are pervaded with uncertainty. Many merging operators have been proposed to deal with this problem in possibilistic logic, a weighted logic which is powerful for handling inconsistency and deal- ing with uncertainty. They often result in a possibilistic knowledge base which is a set of weighted formulas. Although possibilistic logic is inconsistency tolerant, it suers from the well-known "drowning effect". Therefore, we may still want to obtain a consistent possi- bilistic knowledge base as the result of merg- ing. In such a case, we argue that it is not always necessary to keep weighted informa- tion after merging. In this paper, we define a merging operator that maps a set of pos- sibilistic knowledge bases and a formula rep- resenting the integrity constraints to a clas- sical knowledge base by using lexicographic ordering. We show that it satisfies nine pos- tulates that generalize basic postulates for propositional merging given in [11]. These postulates capture the principle of minimal change in some sense. We then provide an algorithm for generating the resulting knowl- edge base of our merging operator. Finally, we discuss the compatibility of our merging operator with propositional merging and es- tablish the advantage of our merging opera- tor over existing semantic merging operators in the propositional case.