Search-Based Online Trajectory Planning for Car-like Robots in Highly Dynamic Environments

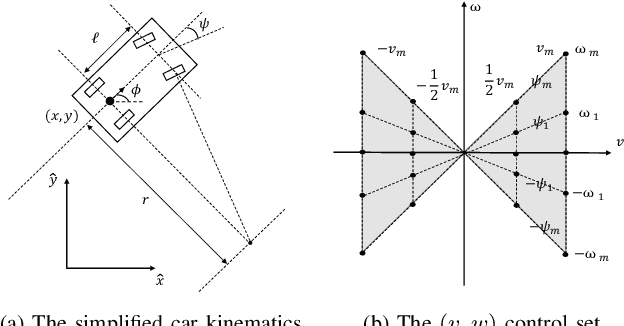
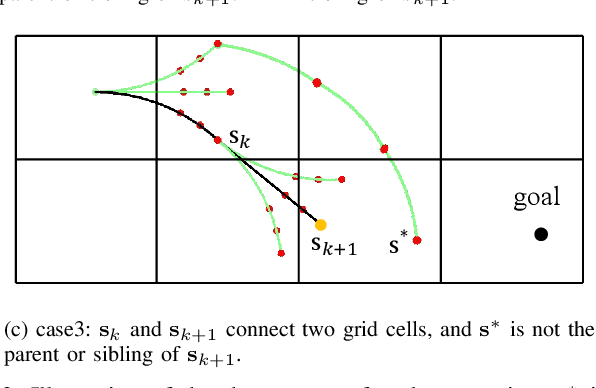
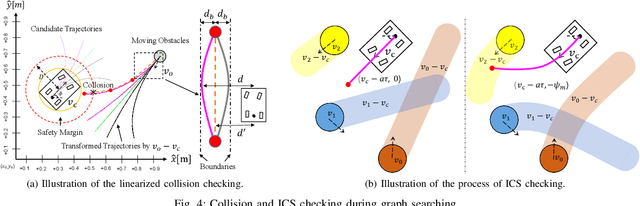
This paper presents a search-based partial motion planner to generate dynamically feasible trajectories for car-like robots in highly dynamic environments. The planner searches for smooth, safe, and near-time-optimal trajectories by exploring a state graph built on motion primitives, which are generated by discretizing the time dimension and the control space. To enable fast online planning, we first propose an efficient path searching algorithm based on the aggregation and pruning of motion primitives. We then propose a fast collision checking algorithm that takes into account the motions of moving obstacles. The algorithm linearizes relative motions between the robot and obstacles and then checks collisions by comparing a point-line distance. Benefiting from the fast searching and collision checking algorithms, the planner can effectively and safely explore the state-time space to generate near-time-optimal solutions. The results through extensive experiments show that the proposed method can generate feasible trajectories within milliseconds while maintaining a higher success rate than up-to-date methods, which significantly demonstrates its advantages.

Online State-Time Trajectory Planning Using Timed-ESDF in Highly Dynamic Environments

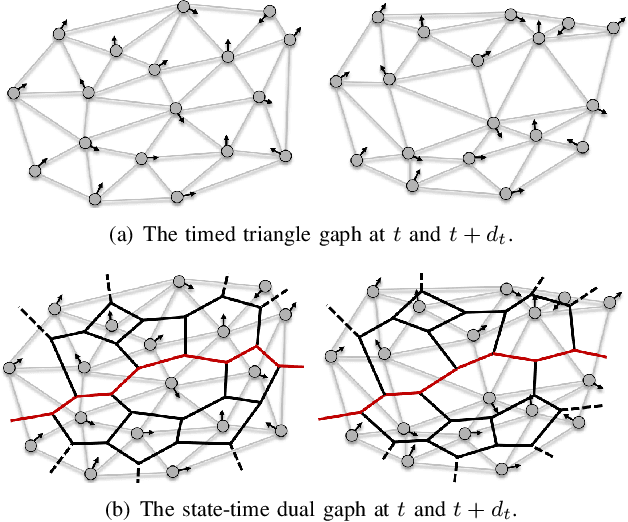
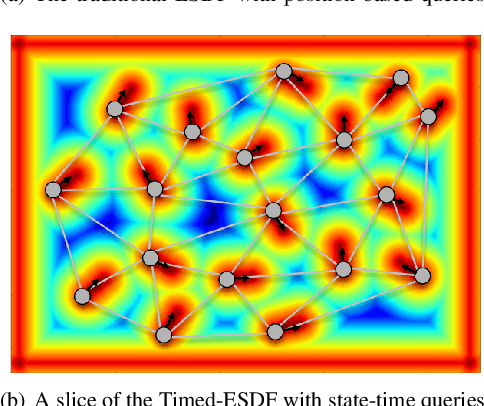
Online state-time trajectory planning in highly dynamic environments remains an unsolved problem due to the unpredictable motions of moving obstacles and the curse of dimensionality from the state-time space. Existing state-time planners are typically implemented based on randomized sampling approaches or path searching on discretized state graph. The smoothness, path clearance, and planning efficiency of these planners are usually not satisfying. In this work, we propose a gradient-based planner over the state-time space for online trajectory generation in highly dynamic environments. To enable the gradient-based optimization, we propose a Timed-ESDT that supports distance and gradient queries with state-time keys. Based on the Timed-ESDT, we also define a smooth prior and an obstacle likelihood function that is compatible with the state-time space. The trajectory planning is then formulated to a MAP problem and solved by an efficient numerical optimizer. Moreover, to improve the optimality of the planner, we also define a state-time graph and then conduct path searching on it to find a better initialization for the optimizer. By integrating the graph searching, the planning quality is significantly improved. Experiment results on simulated and benchmark datasets show that our planner can outperform the state-of-the-art methods, demonstrating its significant advantages over the traditional ones.