Commodification of Compute

The rapid advancements in artificial intelligence, big data analytics, and cloud computing have precipitated an unprecedented demand for computational resources. However, the current landscape of computational resource allocation is characterized by significant inefficiencies, including underutilization and price volatility. This paper addresses these challenges by introducing a novel global platform for the commodification of compute hours, termed the Global Compute Exchange (GCX) (Patent Pending). The GCX leverages blockchain technology and smart contracts to create a secure, transparent, and efficient marketplace for buying and selling computational power. The GCX is built in a layered fashion, comprising Market, App, Clearing, Risk Management, Exchange (Offchain), and Blockchain (Onchain) layers, each ensuring a robust and efficient operation. This platform aims to revolutionize the computational resource market by fostering a decentralized, efficient, and transparent ecosystem that ensures equitable access to computing power, stimulates innovation, and supports diverse user needs on a global scale. By transforming compute hours into a tradable commodity, the GCX seeks to optimize resource utilization, stabilize pricing, and democratize access to computational resources. This paper explores the technological infrastructure, market potential, and societal impact of the GCX, positioning it as a pioneering solution poised to drive the next wave of innovation in commodities and compute.

A Strategy for Adaptive Sampling of Multi-fidelity Gaussian Process to Reduce Predictive Uncertainty

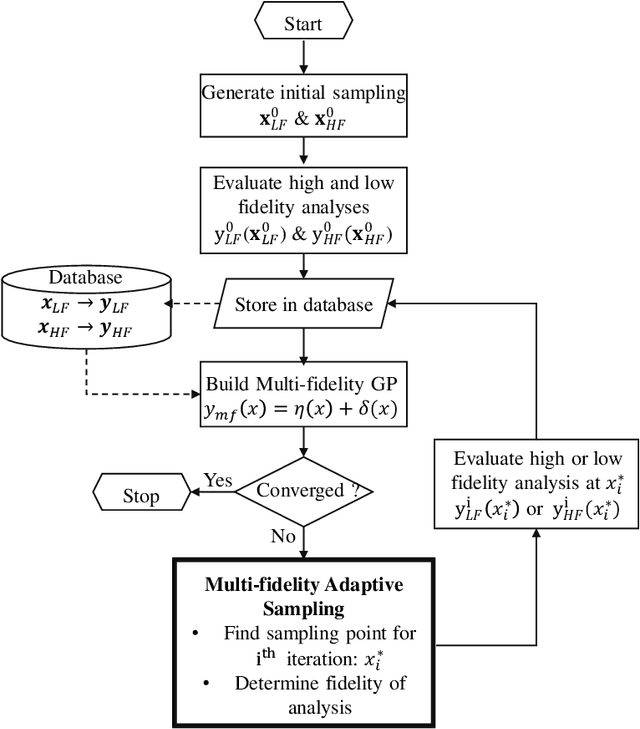
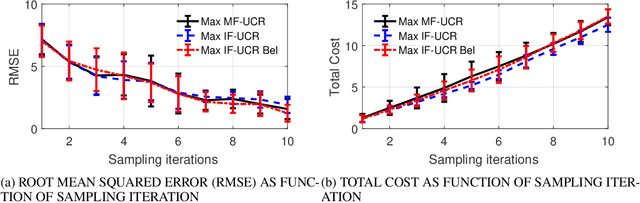
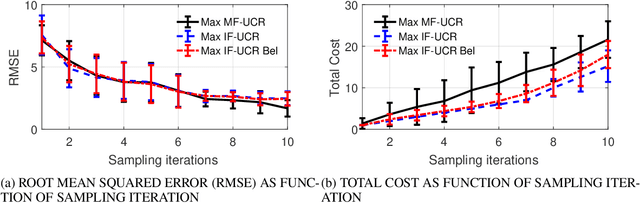
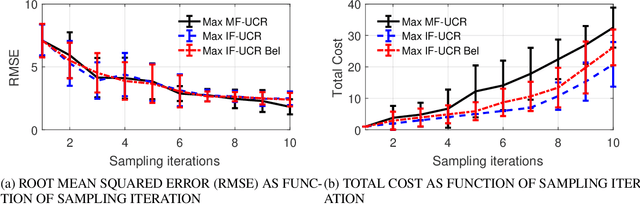
Multi-fidelity Gaussian process is a common approach to address the extensive computationally demanding algorithms such as optimization, calibration and uncertainty quantification. Adaptive sampling for multi-fidelity Gaussian process is a changing task due to the fact that not only we seek to estimate the next sampling location of the design variable, but also the level of the simulator fidelity. This issue is often addressed by including the cost of the simulator as an another factor in the searching criterion in conjunction with the uncertainty reduction metric. In this work, we extent the traditional design of experiment framework for the multi-fidelity Gaussian process by partitioning the prediction uncertainty based on the fidelity level and the associated cost of execution. In addition, we utilize the concept of Believer which quantifies the effect of adding an exploratory design point on the Gaussian process uncertainty prediction. We demonstrated our framework using academic examples as well as a industrial application of steady-state thermodynamic operation point of a fluidized bed process

Towards Scalable Gaussian Process Modeling

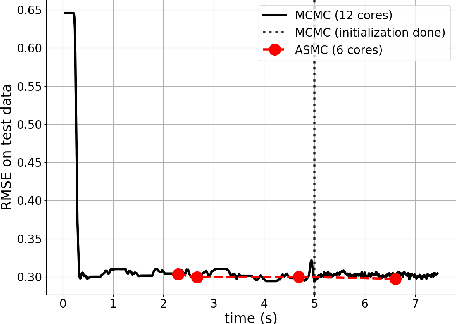
Numerous engineering problems of interest to the industry are often characterized by expensive black-box objective experiments or computer simulations. Obtaining insight into the problem or performing subsequent optimizations requires hundreds of thousands of evaluations of the objective function which is most often a practically unachievable task. Gaussian Process (GP) surrogate modeling replaces the expensive function with a cheap-to-evaluate data-driven probabilistic model. While the GP does not assume a functional form of the problem, it is defined by a set of parameters, called hyperparameters. The hyperparameters define the characteristics of the objective function, such as smoothness, magnitude, periodicity, etc. Accurately estimating these hyperparameters is a key ingredient in developing a reliable and generalizable surrogate model. Markov chain Monte Carlo (MCMC) is a ubiquitously used Bayesian method to estimate these hyperparameters. At the GE Global Research Center, a customized industry-strength Bayesian hybrid modeling framework utilizing the GP, called GEBHM, has been employed and validated over many years. GEBHM is very effective on problems of small and medium size, typically less than 1000 training points. However, the GP does not scale well in time with a growing dataset and problem dimensionality which can be a major impediment in such problems. In this work, we extend and implement in GEBHM an Adaptive Sequential Monte Carlo (ASMC) methodology for training the GP enabling the modeling of large-scale industry problems. This implementation saves computational time (especially for large-scale problems) while not sacrificing predictability over the current MCMC implementation. We demonstrate the effectiveness and accuracy of GEBHM with ASMC on four mathematical problems and on two challenging industry applications of varying complexity.