Riemannian Denoising Score Matching for Molecular Structure Optimization with Accurate Energy

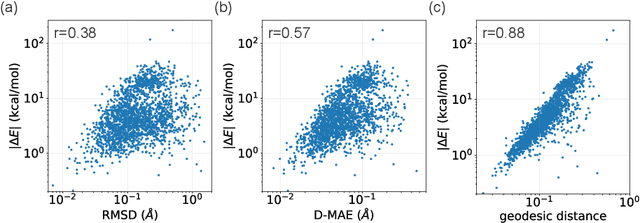
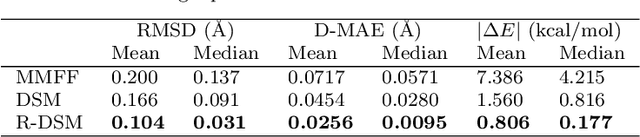
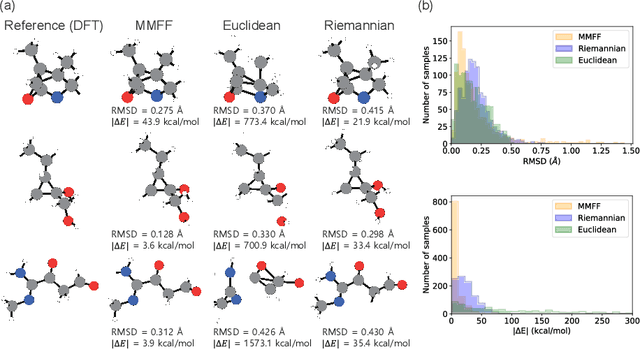
This study introduces a modified score matching method aimed at generating molecular structures with high energy accuracy. The denoising process of score matching or diffusion models mirrors molecular structure optimization, where scores act like physical force fields that guide particles toward equilibrium states. To achieve energetically accurate structures, it can be advantageous to have the score closely approximate the gradient of the actual potential energy surface. Unlike conventional methods that simply design the target score based on structural differences in Euclidean space, we propose a Riemannian score matching approach. This method represents molecular structures on a manifold defined by physics-informed internal coordinates to efficiently mimic the energy landscape, and performs noising and denoising within this space. Our method has been evaluated by refining several types of starting structures on the QM9 and GEOM datasets, demonstrating that the proposed Riemannian score matching method significantly improves the accuracy of the generated molecular structures, attaining chemical accuracy. The implications of this study extend to various applications in computational chemistry, offering a robust tool for accurate molecular structure prediction.

Discrete Diffusion Schrödinger Bridge Matching for Graph Transformation

Transporting between arbitrary distributions is a fundamental goal in generative modeling. Recently proposed diffusion bridge models provide a potential solution, but they rely on a joint distribution that is difficult to obtain in practice. Furthermore, formulations based on continuous domains limit their applicability to discrete domains such as graphs. To overcome these limitations, we propose Discrete Diffusion Schr\"odinger Bridge Matching (DDSBM), a novel framework that utilizes continuous-time Markov chains to solve the SB problem in a high-dimensional discrete state space. Our approach extends Iterative Markovian Fitting to discrete domains, and we have proved its convergence to the SB. Furthermore, we adapt our framework for the graph transformation and show that our design choice of underlying dynamics characterized by independent modifications of nodes and edges can be interpreted as the entropy-regularized version of optimal transport with a cost function described by the graph edit distance. To demonstrate the effectiveness of our framework, we have applied DDSBM to molecular optimization in the field of chemistry. Experimental results demonstrate that DDSBM effectively optimizes molecules' property-of-interest with minimal graph transformation, successfully retaining other features.

A 2D Graph-Based Generative Approach For Exploring Transition States Using Diffusion Model

The exploration of transition state (TS) geometries is crucial for elucidating chemical reaction mechanisms and modeling their kinetics. In recent years, machine learning (ML) models have shown remarkable performance in TS geometry prediction. However, they require 3D geometries of reactants and products that can be challenging to determine. To tackle this, we introduce TSDiff, a novel ML model based on the stochastic diffusion method, which generates the 3D geometry of the TS from a 2D graph composed of molecular connectivity. Despite of this simple input, TSDiff generated TS geometries with high accuracy, outperforming existing ML models that utilize geometric information. Moreover, the generative model approach enabled the sampling of various valid TS conformations, even though only a single conformation for each reaction was used in training. Consequently, TSDiff also found more favorable reaction pathways with lower barrier heights than those in the reference database. We anticipate that this approach will be useful for exploring complex reactions that require the consideration of multiple TS conformations.

Predicting quantum chemical property with easy-to-obtain geometry via positional denoising

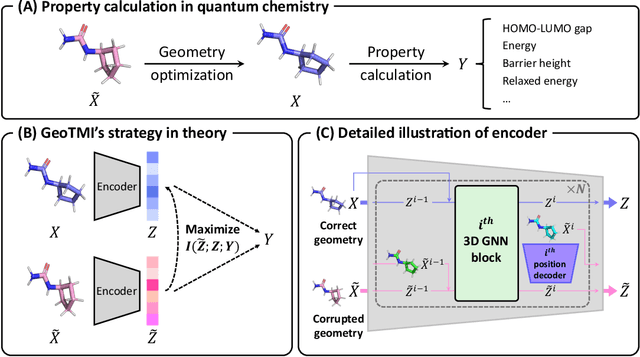
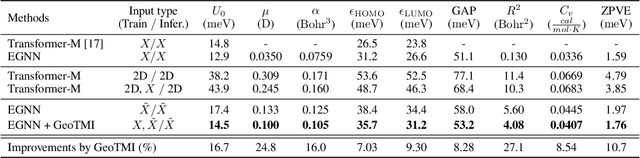
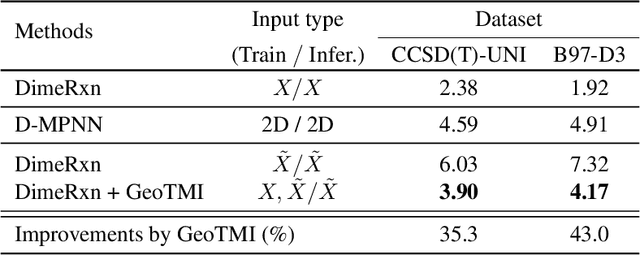
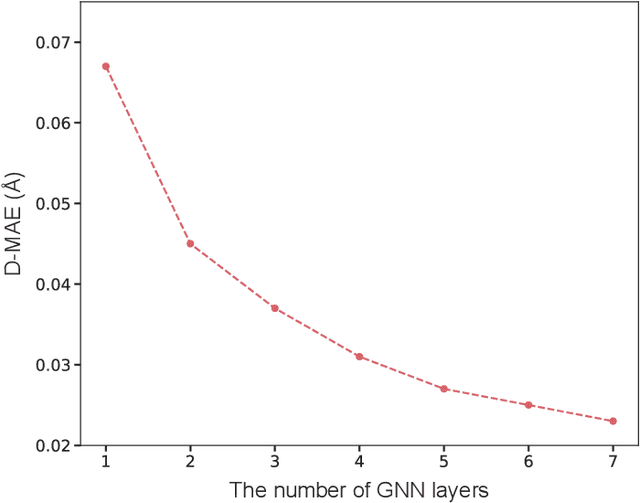
As quantum chemical properties have a significant dependence on their geometries, graph neural networks (GNNs) using 3D geometric information have achieved high prediction accuracy in many tasks. However, they often require 3D geometries obtained from high-level quantum mechanical calculations, which are practically infeasible, limiting their applicability in real-world problems. To tackle this, we propose a method to accurately predict the properties with relatively easy-to-obtain geometries (e.g., optimized geometries from the molecular force field). In this method, the input geometry, regarded as the corrupted geometry of the correct one, gradually approaches the correct one as it passes through the stacked denoising layers. We investigated the performance of the proposed method using 3D message-passing architectures for two prediction tasks: molecular properties and chemical reaction property. The reduction of positional errors through the denoising process contributed to performance improvement by increasing the mutual information between the correct and corrupted geometries. Moreover, our analysis of the correlation between denoising power and predictive accuracy demonstrates the effectiveness of the denoising process.