Domain-Aware Augmentations for Unsupervised Online General Continual Learning

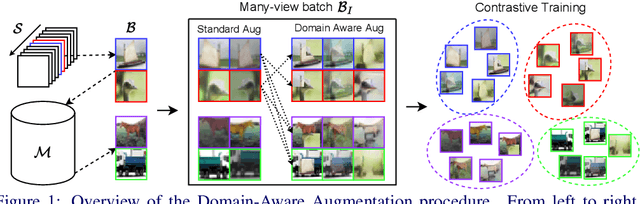
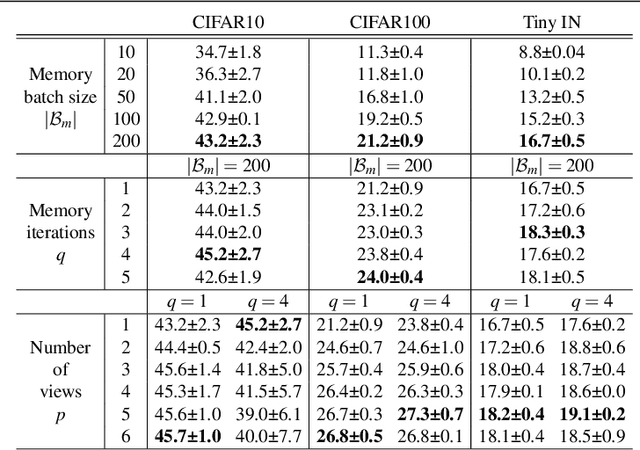
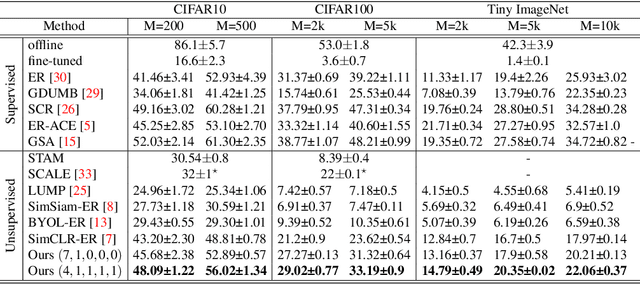
Continual Learning has been challenging, especially when dealing with unsupervised scenarios such as Unsupervised Online General Continual Learning (UOGCL), where the learning agent has no prior knowledge of class boundaries or task change information. While previous research has focused on reducing forgetting in supervised setups, recent studies have shown that self-supervised learners are more resilient to forgetting. This paper proposes a novel approach that enhances memory usage for contrastive learning in UOGCL by defining and using stream-dependent data augmentations together with some implementation tricks. Our proposed method is simple yet effective, achieves state-of-the-art results compared to other unsupervised approaches in all considered setups, and reduces the gap between supervised and unsupervised continual learning. Our domain-aware augmentation procedure can be adapted to other replay-based methods, making it a promising strategy for continual learning.

New metrics for analyzing continual learners

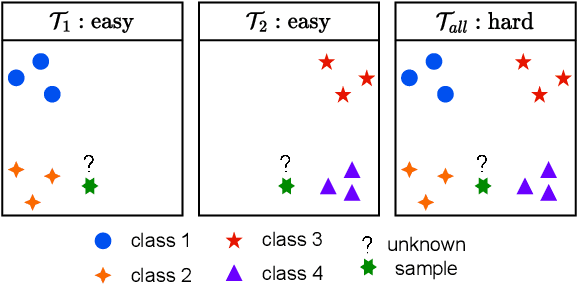
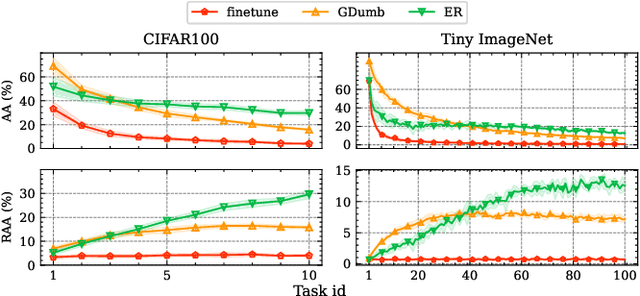
Deep neural networks have shown remarkable performance when trained on independent and identically distributed data from a fixed set of classes. However, in real-world scenarios, it can be desirable to train models on a continuous stream of data where multiple classification tasks are presented sequentially. This scenario, known as Continual Learning (CL) poses challenges to standard learning algorithms which struggle to maintain knowledge of old tasks while learning new ones. This stability-plasticity dilemma remains central to CL and multiple metrics have been proposed to adequately measure stability and plasticity separately. However, none considers the increasing difficulty of the classification task, which inherently results in performance loss for any model. In that sense, we analyze some limitations of current metrics and identify the presence of setup-induced forgetting. Therefore, we propose new metrics that account for the task's increasing difficulty. Through experiments on benchmark datasets, we demonstrate that our proposed metrics can provide new insights into the stability-plasticity trade-off achieved by models in the continual learning environment.

Learning Representations on the Unit Sphere: Application to Online Continual Learning

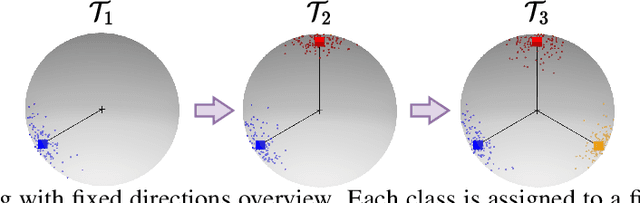
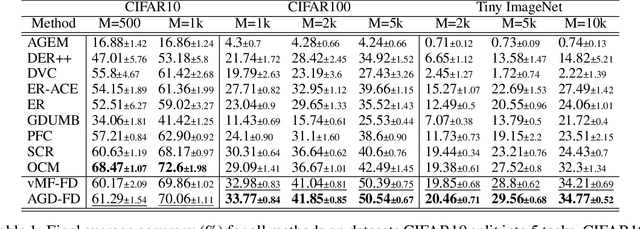
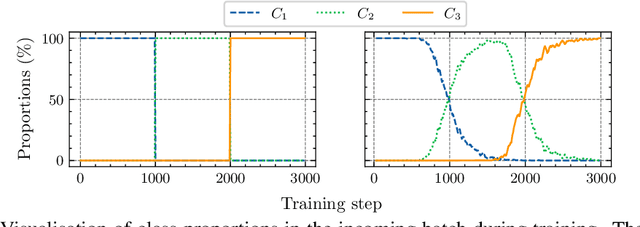
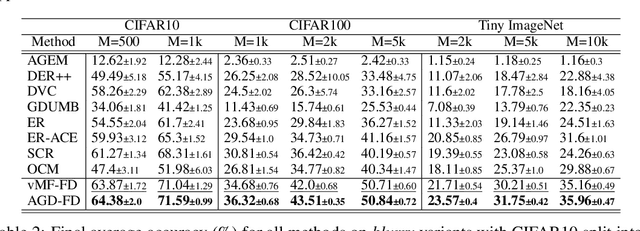
We use the maximum a posteriori estimation principle for learning representations distributed on the unit sphere. We derive loss functions for the von Mises-Fisher distribution and the angular Gaussian distribution, both designed for modeling symmetric directional data. A noteworthy feature of our approach is that the learned representations are pushed toward fixed directions, allowing for a learning strategy that is resilient to data drift. This makes it suitable for online continual learning, which is the problem of training neural networks on a continuous data stream, where multiple classification tasks are presented sequentially so that data from past tasks are no longer accessible, and data from the current task can be seen only once. To address this challenging scenario, we propose a memory-based representation learning technique equipped with our new loss functions. Our approach does not require negative data or knowledge of task boundaries and performs well with smaller batch sizes while being computationally efficient. We demonstrate with extensive experiments that the proposed method outperforms the current state-of-the-art methods on both standard evaluation scenarios and realistic scenarios with blurry task boundaries. For reproducibility, we use the same training pipeline for every compared method and share the code at https://t.ly/SQTj.

Low Complexity Adaptive Machine Learning Approaches for End-to-End Latency Prediction

Software Defined Networks have opened the door to statistical and AI-based techniques to improve efficiency of networking. Especially to ensure a certain Quality of Service (QoS) for specific applications by routing packets with awareness on content nature (VoIP, video, files, etc.) and its needs (latency, bandwidth, etc.) to use efficiently resources of a network. Monitoring and predicting various Key Performance Indicators (KPIs) at any level may handle such problems while preserving network bandwidth. The question addressed in this work is the design of efficient, low-cost adaptive algorithms for KPI estimation, monitoring and prediction. We focus on end-to-end latency prediction, for which we illustrate our approaches and results on data obtained from a public generator provided after the recent international challenge on GNN [12]. In this paper, we improve our previously proposed low-cost estimators [6] by adding the adaptive dimension, and show that the performances are minimally modified while gaining the ability to track varying networks.

Low Complexity Approaches for End-to-End Latency Prediction

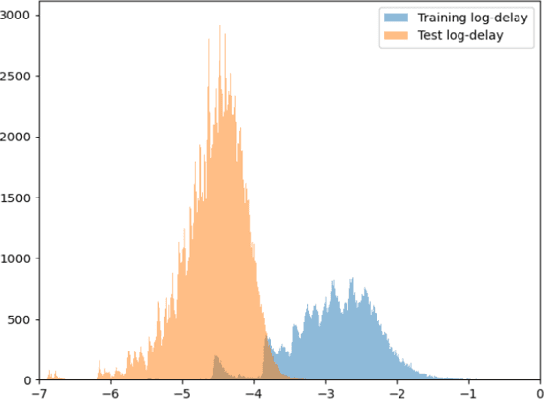
Software Defined Networks have opened the door to statistical and AI-based techniques to improve efficiency of networking. Especially to ensure a certain Quality of Service (QoS) for specific applications by routing packets with awareness on content nature (VoIP, video, files, etc.) and its needs (latency, bandwidth, etc.) to use efficiently resources of a network. Predicting various Key Performance Indicators (KPIs) at any level may handle such problems while preserving network bandwidth. The question addressed in this work is the design of efficient and low-cost algorithms for KPI prediction, implementable at the local level. We focus on end-to-end latency prediction, for which we illustrate our approaches and results on a public dataset from the recent international challenge on GNN [1]. We propose several low complexity, locally implementable approaches, achieving significantly lower wall time both for training and inference, with marginally worse prediction accuracy compared to state-of-the-art global GNN solutions.

Contrastive Learning for Online Semi-Supervised General Continual Learning

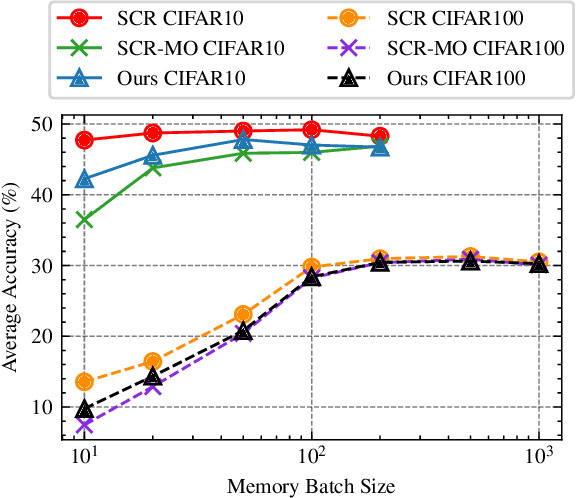
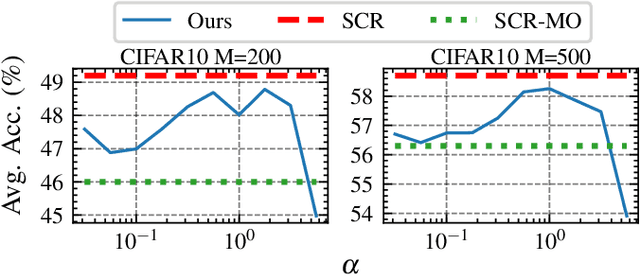
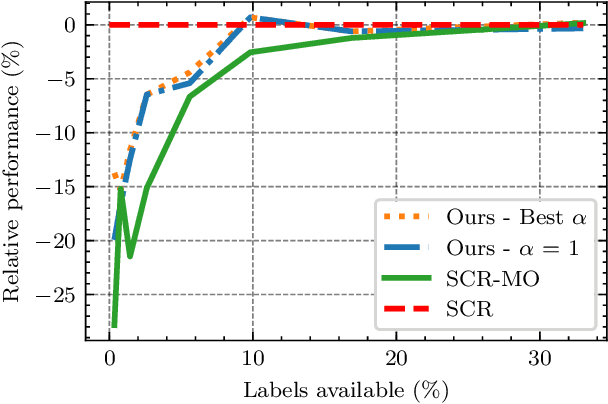
We study Online Continual Learning with missing labels and propose SemiCon, a new contrastive loss designed for partly labeled data. We demonstrate its efficiency by devising a memory-based method trained on an unlabeled data stream, where every data added to memory is labeled using an oracle. Our approach outperforms existing semi-supervised methods when few labels are available, and obtain similar results to state-of-the-art supervised methods while using only 2.6% of labels on Split-CIFAR10 and 10% of labels on Split-CIFAR100.

On some interrelations of generalized $q$-entropies and a generalized Fisher information, including a Cramér-Rao inequality

In this communication, we describe some interrelations between generalized $q$-entropies and a generalized version of Fisher information. In information theory, the de Bruijn identity links the Fisher information and the derivative of the entropy. We show that this identity can be extended to generalized versions of entropy and Fisher information. More precisely, a generalized Fisher information naturally pops up in the expression of the derivative of the Tsallis entropy. This generalized Fisher information also appears as a special case of a generalized Fisher information for estimation problems. Indeed, we derive here a new Cram\'er-Rao inequality for the estimation of a parameter, which involves a generalized form of Fisher information. This generalized Fisher information reduces to the standard Fisher information as a particular case. In the case of a translation parameter, the general Cram\'er-Rao inequality leads to an inequality for distributions which is saturated by generalized $q$-Gaussian distributions. These generalized $q$-Gaussians are important in several areas of physics and mathematics. They are known to maximize the $q$-entropies subject to a moment constraint. The Cram\'er-Rao inequality shows that the generalized $q$-Gaussians also minimize the generalized Fisher information among distributions with a fixed moment. Similarly, the generalized $q$-Gaussians also minimize the generalized Fisher information among distributions with a given $q$-entropy.

Some results on a $χ$-divergence, an~extended~Fisher information and~generalized~Cramér-Rao inequalities

We propose a modified $\chi^{\beta}$-divergence, give some of its properties, and show that this leads to the definition of a generalized Fisher information. We give generalized Cram\'er-Rao inequalities, involving this Fisher information, an extension of the Fisher information matrix, and arbitrary norms and power of the estimation error. In the case of a location parameter, we obtain new characterizations of the generalized $q$-Gaussians, for instance as the distribution with a given moment that minimizes the generalized Fisher information. Finally we indicate how the generalized Fisher information can lead to new uncertainty relations.