REST: Retrieval-Based Speculative Decoding

We introduce Retrieval-Based Speculative Decoding (REST), a novel algorithm designed to speed up language model generation. The key insight driving the development of REST is the observation that the process of text generation often includes certain common phases and patterns. Unlike previous methods that rely on a draft language model for speculative decoding, REST harnesses the power of retrieval to generate draft tokens. This method draws from the reservoir of existing knowledge, retrieving and employing relevant tokens based on the current context. Its plug-and-play nature allows for seamless integration and acceleration of any language models, all without necessitating additional training. When benchmarked on 7B and 13B language models in a single-batch setting, REST achieves a significant speedup of 1.62X to 2.36X on code or text generation. The code of REST is available at https://github.com/FasterDecoding/REST.

Exact Post Model Selection Inference for Marginal Screening

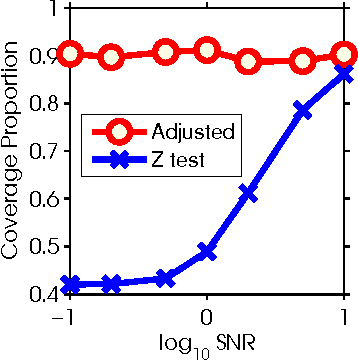
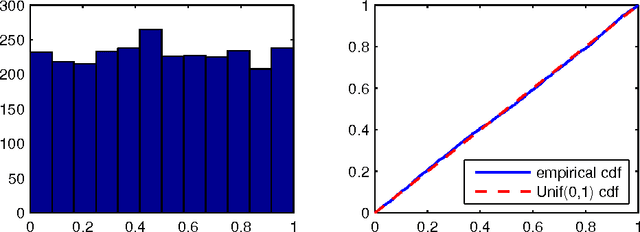
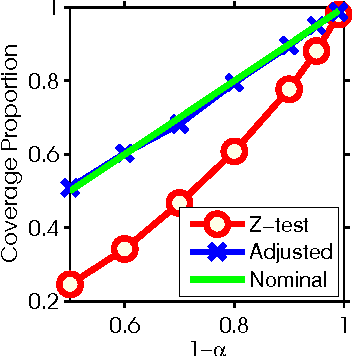
We develop a framework for post model selection inference, via marginal screening, in linear regression. At the core of this framework is a result that characterizes the exact distribution of linear functions of the response $y$, conditional on the model being selected (``condition on selection" framework). This allows us to construct valid confidence intervals and hypothesis tests for regression coefficients that account for the selection procedure. In contrast to recent work in high-dimensional statistics, our results are exact (non-asymptotic) and require no eigenvalue-like assumptions on the design matrix $X$. Furthermore, the computational cost of marginal regression, constructing confidence intervals and hypothesis testing is negligible compared to the cost of linear regression, thus making our methods particularly suitable for extremely large datasets. Although we focus on marginal screening to illustrate the applicability of the condition on selection framework, this framework is much more broadly applicable. We show how to apply the proposed framework to several other selection procedures including orthogonal matching pursuit, non-negative least squares, and marginal screening+Lasso.

Using Multiple Samples to Learn Mixture Models

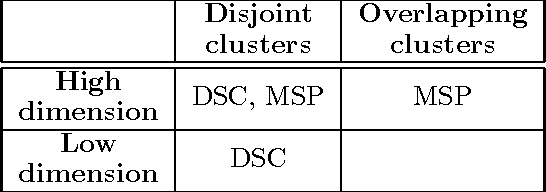
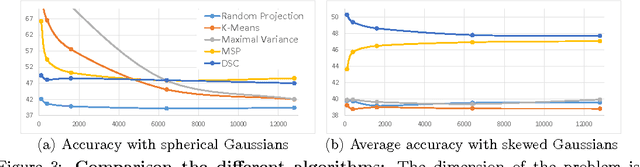
In the mixture models problem it is assumed that there are $K$ distributions $\theta_{1},\ldots,\theta_{K}$ and one gets to observe a sample from a mixture of these distributions with unknown coefficients. The goal is to associate instances with their generating distributions, or to identify the parameters of the hidden distributions. In this work we make the assumption that we have access to several samples drawn from the same $K$ underlying distributions, but with different mixing weights. As with topic modeling, having multiple samples is often a reasonable assumption. Instead of pooling the data into one sample, we prove that it is possible to use the differences between the samples to better recover the underlying structure. We present algorithms that recover the underlying structure under milder assumptions than the current state of art when either the dimensionality or the separation is high. The methods, when applied to topic modeling, allow generalization to words not present in the training data.