Distributed Multirobot Control for Non-Cooperative Herding

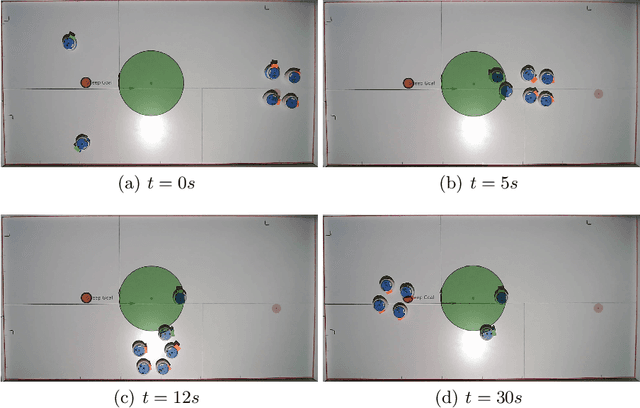
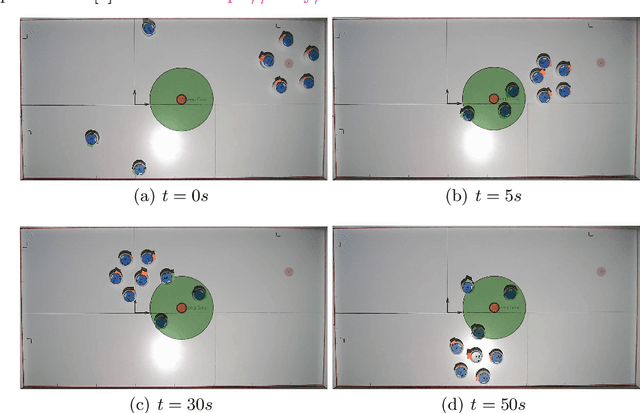
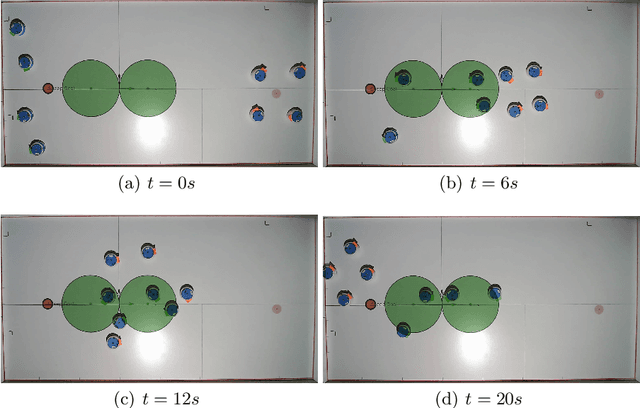
In this paper, we consider the problem of protecting a high-value area from being breached by sheep agents by crafting motions for dog robots. We use control barrier functions to pose constraints on the dogs' velocities that induce repulsions in the sheep relative to the high-value area. This paper extends the results developed in our prior work on the same topic in three ways. Firstly, we implement and validate our previously developed centralized herding algorithm on many robots. We show herding of up to five sheep agents using three dog robots. Secondly, as an extension to the centralized approach, we develop two distributed herding algorithms, one favoring feasibility while the other favoring optimality. In the first algorithm, we allocate a unique sheep to a unique dog, making that dog responsible for herding its allocated sheep away from the protected zone. We provide feasibility proof for this approach, along with numerical simulations. In the second algorithm, we develop an iterative distributed reformulation of the centralized algorithm, which inherits the optimality (i.e. budget efficiency) from the centralized approach. Lastly, we conduct real-world experiments of these distributed algorithms and demonstrate herding of up to five sheep agents using five dog robots.

The Before, During, and After of Multi-Robot Deadlock

Collision avoidance for multirobot systems is a well-studied problem. Recently, control barrier functions (CBFs) have been proposed for synthesizing controllers that guarantee collision avoidance and goal stabilization for multiple robots. However, it has been noted that reactive control synthesis methods (such as CBFs) are prone to \textit{deadlock}, an equilibrium of system dynamics that causes the robots to stall before reaching their goals. In this paper, we analyze the closed-loop dynamics of robots using CBFs, to characterize controller parameters, initial conditions, and goal locations that invariably lead the system to deadlock. Using tools from duality theory, we derive geometric properties of robot configurations of an $N$ robot system once it is in deadlock and we justify them using the mechanics interpretation of KKT conditions. Our key deductions are that 1) system deadlock is characterized by a force-equilibrium on robots and 2) deadlock occurs to ensure safety when safety is on the brink of being violated. These deductions allow us to interpret deadlock as a subset of the state space, and we show that this set is non-empty and located on the boundary of the safe set. By exploiting these properties, we analyze the number of admissible robot configurations in deadlock and develop a provably-correct decentralized algorithm for deadlock resolution to safely deliver the robots to their goals. This algorithm is validated in simulations as well as experimentally on Khepera-IV robots.

Noncooperative Herding With Control Barrier Functions: Theory and Experiments

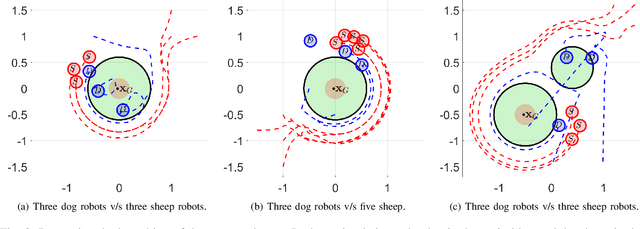
In this paper, we consider the problem of protecting a high-value unit from inadvertent attack by a group of agents using defending robots. Specifically, we develop a control strategy for the defending agents that we call "dog robots" to prevent a flock of "sheep agents" from breaching a protected zone. We take recourse to control barrier functions to pose this problem and exploit the interaction dynamics between the sheep and dogs to find dogs' velocities that result in the sheep getting repelled from the zone. We solve a QP reactively that incorporates the defending constraints to compute the desired velocities for all dogs. Owing to this, our proposed framework is composable \textit{i.e.} it allows for simultaneous inclusion of multiple protected zones in the constraints on dog robots' velocities. We provide a theoretical proof of feasibility of our strategy for the one dog/one sheep case. Additionally, we provide empirical results of two dogs defending the protected zone from upto ten sheep averaged over a hundred simulations and report high success rates. We also demonstrate this algorithm experimentally on non-holonomic robots. Videos of these results are available at https://tinyurl.com/4dj2kjwx.

Feasible Region-based Identification Using Duality (Extended Version)

We consider the problem of estimating bounds on parameters representing tasks being performed by individual robots in a multirobot system. In our previous work, we derived necessary conditions based on persistency of excitation analysis for the exact identification of these parameters. We concluded that depending on the robot's task, the dynamics of individual robots may fail to satisfy these conditions, thereby preventing exact inference. As an extension to that work, this paper focuses on estimating bounds on task parameters when such conditions are not satisfied. Each robot in the team uses optimization-based controllers for mediating between task satisfaction and collision avoidance. We use KKT conditions of this optimization and SVD of active collision avoidance constraints to derive explicit relations between Lagrange multipliers, robot dynamics, and task parameters. Using these relations, we are able to derive bounds on each robot's task parameters. Through numerical simulations, we show how our proposed region based identification approach generates feasible regions for parameters when a conventional estimator such as a UKF fails. Additionally, empirical evidence shows that this approach generates contracting sets which converge to the true parameters much faster than the rate at which a UKF based estimate converges. Videos of these results are available at https://bit.ly/2JDMgeJ

Deadlock Analysis and Resolution in Multi-Robot Systems: The Two Robot Case

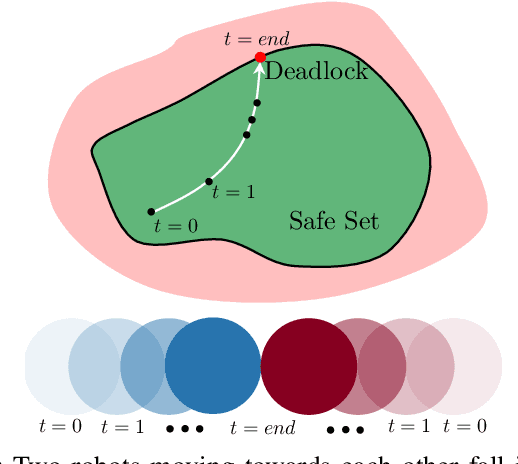
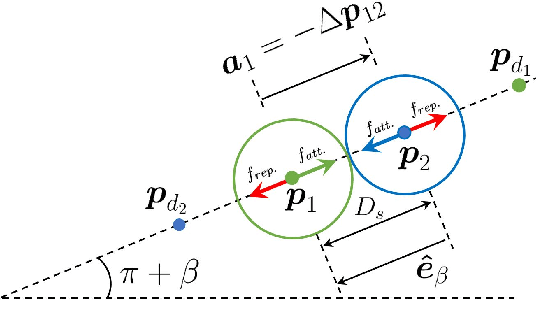
Collision avoidance for multirobot systems is a well studied problem. Recently, control barrier functions (CBFs) have been proposed for synthesizing decentralized controllers that guarantee collision avoidance (safety) and goal stabilization (performance) for multiple robots. However, it has been noted in several works that reactive control synthesis methods (such as CBFs) are prone to deadlock, an equilibrium of system dynamics that causes the robots to come to a standstill before they reach their goals. In this paper, we analyze the incidence of deadlocks in a multirobot system that uses CBFs for goal stabilization and collision avoidance. Our analysis is formal, in that we demonstrate that system deadlock is indeed the result of a force-equilibrium on robots. We show how to interpret deadlock as a subset of the state space and prove that this set is non-empty, bounded, of measure zero and located on the boundary of the safe set. Based on this analysis, we develop a decentralized three-phase algorithm that uses feedback linearization to ensure that the robots provably exit the deadlock set and converge to their goals while avoiding collisions. We show simulation results and experimentally validate the deadlock resolution algorithm on Khepera-IV robots.