Deadlock Analysis and Resolution in Multi-Robot Systems: The Two Robot Case
Paper and Code
Nov 20, 2019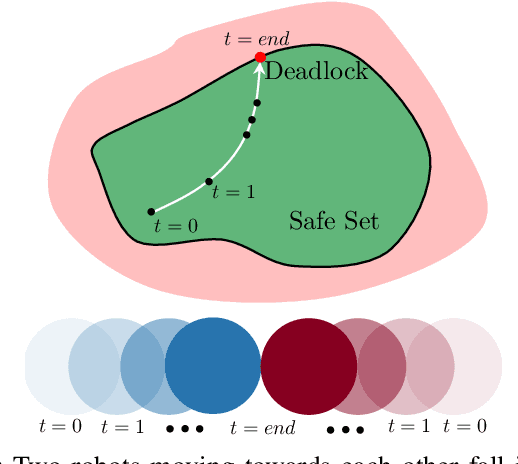

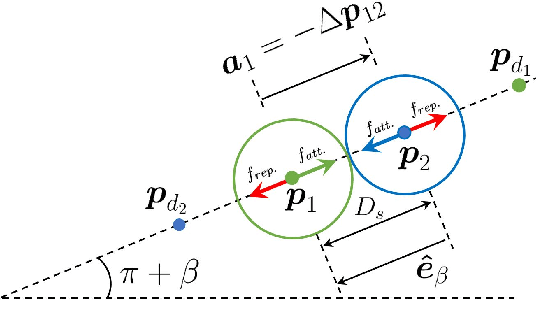

Collision avoidance for multirobot systems is a well studied problem. Recently, control barrier functions (CBFs) have been proposed for synthesizing decentralized controllers that guarantee collision avoidance (safety) and goal stabilization (performance) for multiple robots. However, it has been noted in several works that reactive control synthesis methods (such as CBFs) are prone to deadlock, an equilibrium of system dynamics that causes the robots to come to a standstill before they reach their goals. In this paper, we analyze the incidence of deadlocks in a multirobot system that uses CBFs for goal stabilization and collision avoidance. Our analysis is formal, in that we demonstrate that system deadlock is indeed the result of a force-equilibrium on robots. We show how to interpret deadlock as a subset of the state space and prove that this set is non-empty, bounded, of measure zero and located on the boundary of the safe set. Based on this analysis, we develop a decentralized three-phase algorithm that uses feedback linearization to ensure that the robots provably exit the deadlock set and converge to their goals while avoiding collisions. We show simulation results and experimentally validate the deadlock resolution algorithm on Khepera-IV robots.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge