Jarvis Schultz
Efficient Computation of Higher-Order Variational Integrators in Robotic Simulation and Trajectory Optimization
Apr 29, 2019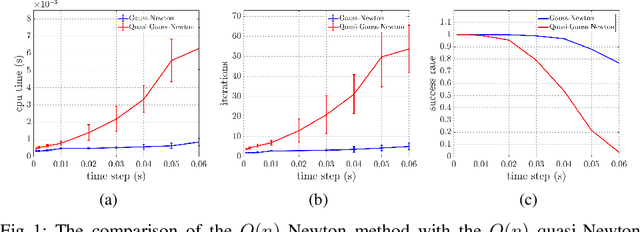
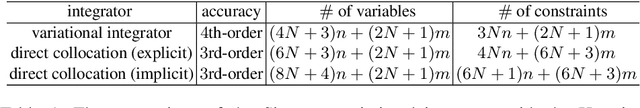
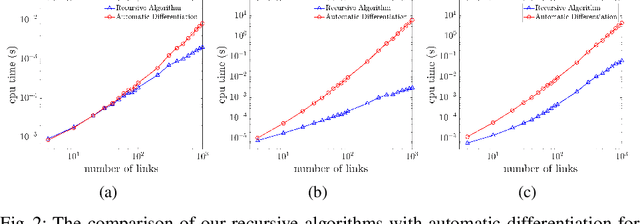
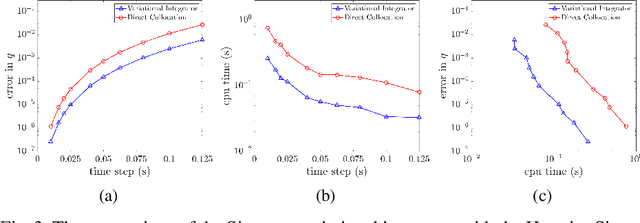
Abstract:This paper addresses the problem of efficiently computing higher-order variational integrators in simulation and trajectory optimization of mechanical systems as those often found in robotic applications. We develop $O(n)$ algorithms to evaluate the discrete Euler-Lagrange (DEL) equations and compute the Newton direction for solving the DEL equations, which results in linear-time variational integrators of arbitrarily high order. To our knowledge, no linear-time higher-order variational or even implicit integrators have been developed before. Moreover, an $O(n^2)$ algorithm to linearize the DEL equations is presented, which is useful for trajectory optimization. These proposed algorithms eliminate the bottleneck of implementing higher-order variational integrators in simulation and trajectory optimization of complex robotic systems. The efficacy of this paper is validated through comparison with existing methods, and implementation on various robotic systems---including trajectory optimization of the Spring Flamingo robot, the LittleDog robot and the Atlas robot. The results illustrate that the same integrator can be used for simulation and trajectory optimization in robotics, preserving mechanical properties while achieving good scalability and accuracy.
* 42 pages, includes appendix
Autonomous Visual Rendering using Physical Motion
Sep 08, 2017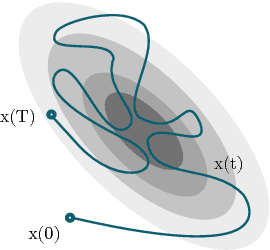
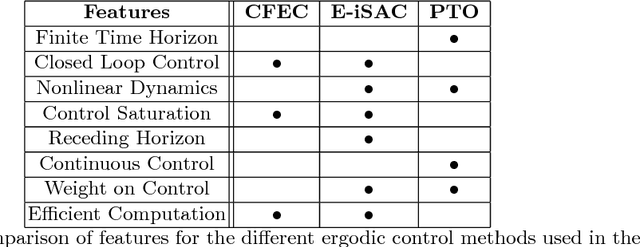


Abstract:This paper addresses the problem of enabling a robot to represent and recreate visual information through physical motion, focusing on drawing using pens, brushes, or other tools. This work uses ergodicity as a control objective that translates planar visual input to physical motion without preprocessing (e.g., image processing, motion primitives). % or human-generated training data (i.e., machine learning). We achieve comparable results to existing drawing methods, while reducing the algorithmic complexity of the software. We demonstrate that optimal ergodic control algorithms with different time-horizon characteristics (infinitesimal, finite, and receding horizon) can generate qualitatively and stylistically different motions that render a wide range of visual information (e.g., letters, portraits, landscapes). In addition, we show that ergodic control enables the same software design to apply to multiple robotic systems by incorporating their particular dynamics, thereby reducing the dependence on task-specific robots. Finally, we demonstrate physical drawings with the Baxter robot.
* 16 pages, to appear in Proceedings of the Workshop on the Algorithmic Foundations of Robotics (WAFR), 2016
Structured Linearization of Discrete Mechanical Systems for Analysis and Optimal Control
Aug 31, 2017
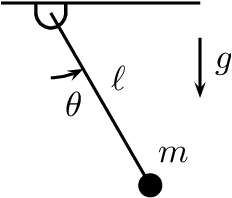
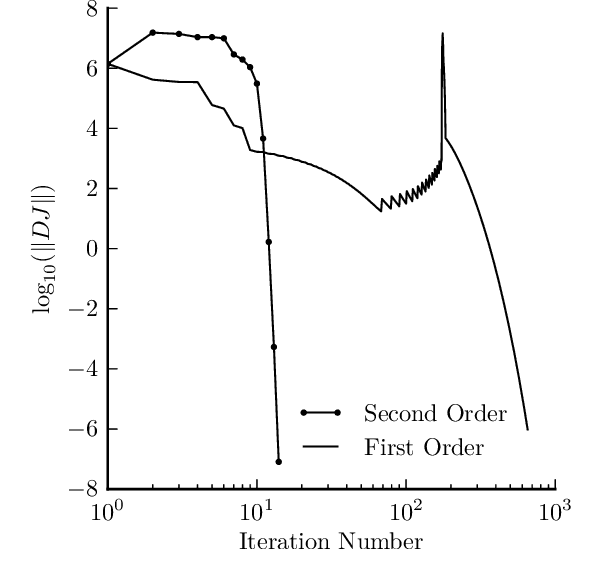
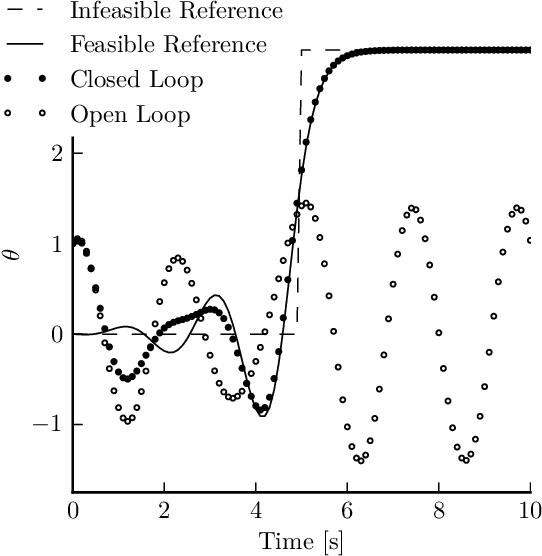
Abstract:Variational integrators are well-suited for simulation of mechanical systems because they preserve mechanical quantities about a system such as momentum, or its change if external forcing is involved, and holonomic constraints. While they are not energy-preserving they do exhibit long-time stable energy behavior. However, variational integrators often simulate mechanical system dynamics by solving an implicit difference equation at each time step, one that is moreover expressed purely in terms of configurations at different time steps. This paper formulates the first- and second-order linearizations of a variational integrator in a manner that is amenable to control analysis and synthesis, creating a bridge between existing analysis and optimal control tools for discrete dynamic systems and variational integrators for mechanical systems in generalized coordinates with forcing and holonomic constraints. The forced pendulum is used to illustrate the technique. A second example solves the discrete LQR problem to find a locally stabilizing controller for a 40 DOF system with 6 constraints.
* 13 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge