Learning payoffs while routing in skill-based queues

Motivated by applications in service systems, we consider queueing systems where each customer must be handled by a server with the right skill set. We focus on optimizing the routing of customers to servers in order to maximize the total payoff of customer--server matches. In addition, customer--server dependent payoff parameters are assumed to be unknown a priori. We construct a machine learning algorithm that adaptively learns the payoff parameters while maximizing the total payoff and prove that it achieves polylogarithmic regret. Moreover, we show that the algorithm is asymptotically optimal up to logarithmic terms by deriving a regret lower bound. The algorithm leverages the basic feasible solutions of a static linear program as the action space. The regret analysis overcomes the complex interplay between queueing and learning by analyzing the convergence of the queue length process to its stationary behavior. We also demonstrate the performance of the algorithm numerically, and have included an experiment with time-varying parameters highlighting the potential of the algorithm in non-static environments.

Estimating the number of clusters of a Block Markov Chain

Clustering algorithms frequently require the number of clusters to be chosen in advance, but it is usually not clear how to do this. To tackle this challenge when clustering within sequential data, we present a method for estimating the number of clusters when the data is a trajectory of a Block Markov Chain. Block Markov Chains are Markov Chains that exhibit a block structure in their transition matrix. The method considers a matrix that counts the number of transitions between different states within the trajectory, and transforms this into a spectral embedding whose dimension is set via singular value thresholding. The number of clusters is subsequently estimated via density-based clustering of this spectral embedding, an approach inspired by literature on the Stochastic Block Model. By leveraging and augmenting recent results on the spectral concentration of random matrices with Markovian dependence, we show that the method is asymptotically consistent - in spite of the dependencies between the count matrix's entries, and even when the count matrix is sparse. We also present a numerical evaluation of our method, and compare it to alternatives.

Score-Aware Policy-Gradient Methods and Performance Guarantees using Local Lyapunov Conditions: Applications to Product-Form Stochastic Networks and Queueing Systems

Stochastic networks and queueing systems often lead to Markov decision processes (MDPs) with large state and action spaces as well as nonconvex objective functions, which hinders the convergence of many reinforcement learning (RL) algorithms. Policy-gradient methods perform well on MDPs with large state and action spaces, but they sometimes experience slow convergence due to the high variance of the gradient estimator. In this paper, we show that some of these difficulties can be circumvented by exploiting the structure of the underlying MDP. We first introduce a new family of gradient estimators called score-aware gradient estimators (SAGEs). When the stationary distribution of the MDP belongs to an exponential family parametrized by the policy parameters, SAGEs allow us to estimate the policy gradient without relying on value-function estimation, contrary to classical policy-gradient methods like actor-critic. To demonstrate their applicability, we examine two common control problems arising in stochastic networks and queueing systems whose stationary distributions have a product-form, a special case of exponential families. As a second contribution, we show that, under appropriate assumptions, the policy under a SAGE-based policy-gradient method has a large probability of converging to an optimal policy, provided that it starts sufficiently close to it, even with a nonconvex objective function and multiple maximizers. Our key assumptions are that, locally around a maximizer, a nondegeneracy property of the Hessian of the objective function holds and a Lyapunov function exists. Finally, we conduct a numerical comparison between a SAGE-based policy-gradient method and an actor-critic algorithm. The results demonstrate that the SAGE-based method finds close-to-optimal policies more rapidly, highlighting its superior performance over the traditional actor-critic method.

Noise-Resilient Designs for Optical Neural Networks

All analog signal processing is fundamentally subject to noise, and this is also the case in modern implementations of Optical Neural Networks (ONNs). Therefore, to mitigate noise in ONNs, we propose two designs that are constructed from a given, possibly trained, Neural Network (NN) that one wishes to implement. Both designs have the capability that the resulting ONNs gives outputs close to the desired NN. To establish the latter, we analyze the designs mathematically. Specifically, we investigate a probabilistic framework for the first design that establishes that the design is correct, i.e., for any feed-forward NN with Lipschitz continuous activation functions, an ONN can be constructed that produces output arbitrarily close to the original. ONNs constructed with the first design thus also inherit the universal approximation property of NNs. For the second design, we restrict the analysis to NNs with linear activation functions and characterize the ONNs' output distribution using exact formulas. Finally, we report on numerical experiments with LeNet ONNs that give insight into the number of components required in these designs for certain accuracy gains. We specifically study the effect of noise as a function of the depth of an ONN. The results indicate that in practice, adding just a few components in the manner of the first or the second design can already be expected to increase the accuracy of ONNs considerably.

Detection and Evaluation of Clusters within Sequential Data

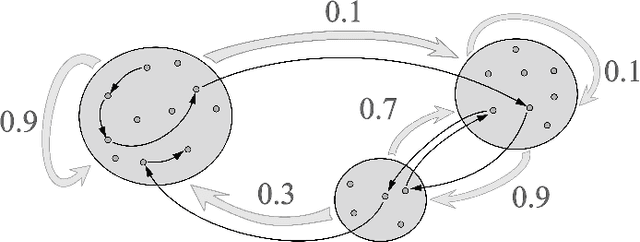
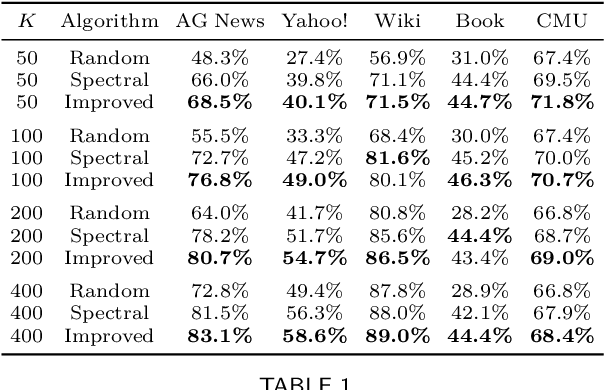
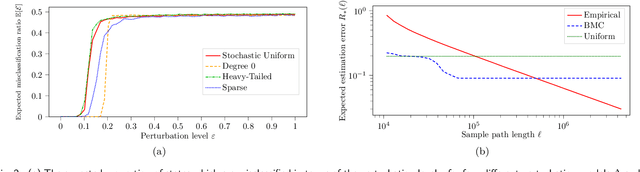
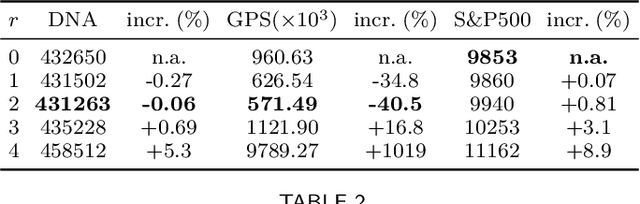
Motivated by theoretical advancements in dimensionality reduction techniques we use a recent model, called Block Markov Chains, to conduct a practical study of clustering in real-world sequential data. Clustering algorithms for Block Markov Chains possess theoretical optimality guarantees and can be deployed in sparse data regimes. Despite these favorable theoretical properties, a thorough evaluation of these algorithms in realistic settings has been lacking. We address this issue and investigate the suitability of these clustering algorithms in exploratory data analysis of real-world sequential data. In particular, our sequential data is derived from human DNA, written text, animal movement data and financial markets. In order to evaluate the determined clusters, and the associated Block Markov Chain model, we further develop a set of evaluation tools. These tools include benchmarking, spectral noise analysis and statistical model selection tools. An efficient implementation of the clustering algorithm and the new evaluation tools is made available together with this paper. Practical challenges associated to real-world data are encountered and discussed. It is ultimately found that the Block Markov Chain model assumption, together with the tools developed here, can indeed produce meaningful insights in exploratory data analyses despite the complexity and sparsity of real-world data.

Universal Approximation in Dropout Neural Networks

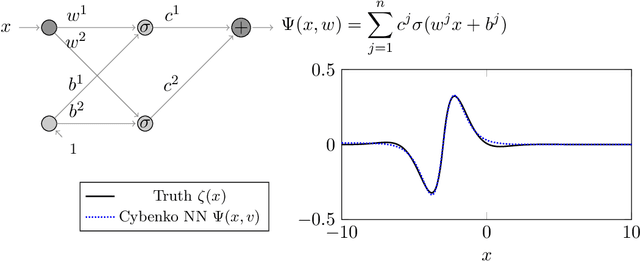
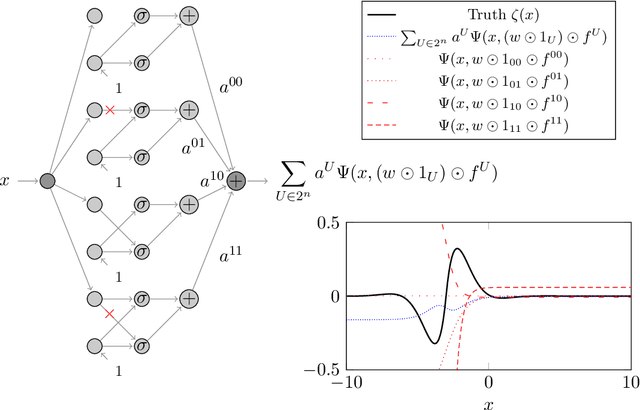
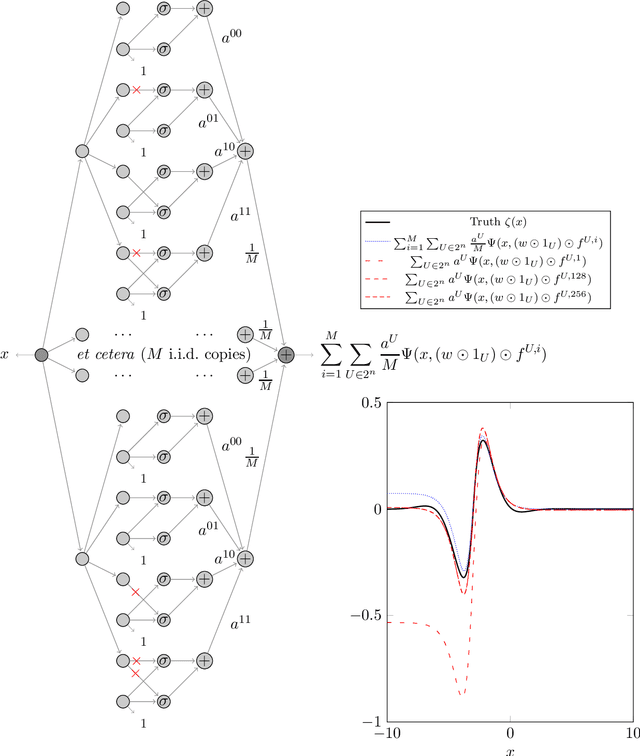
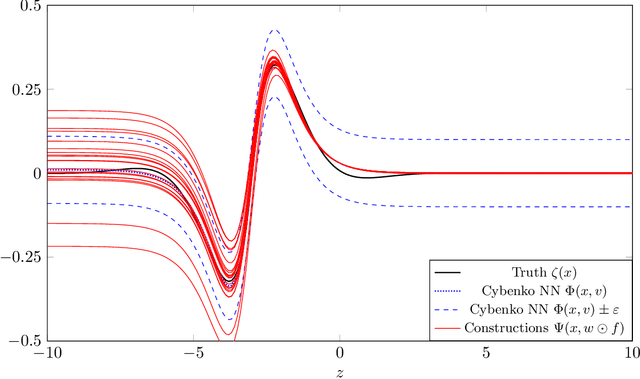
We prove two universal approximation theorems for a range of dropout neural networks. These are feed-forward neural networks in which each edge is given a random $\{0,1\}$-valued filter, that have two modes of operation: in the first each edge output is multiplied by its random filter, resulting in a random output, while in the second each edge output is multiplied by the expectation of its filter, leading to a deterministic output. It is common to use the random mode during training and the deterministic mode during testing and prediction. Both theorems are of the following form: Given a function to approximate and a threshold $\varepsilon>0$, there exists a dropout network that is $\varepsilon$-close in probability and in $L^q$. The first theorem applies to dropout networks in the random mode. It assumes little on the activation function, applies to a wide class of networks, and can even be applied to approximation schemes other than neural networks. The core is an algebraic property that shows that deterministic networks can be exactly matched in expectation by random networks. The second theorem makes stronger assumptions and gives a stronger result. Given a function to approximate, it provides existence of a network that approximates in both modes simultaneously. Proof components are a recursive replacement of edges by independent copies, and a special first-layer replacement that couples the resulting larger network to the input. The functions to be approximated are assumed to be elements of general normed spaces, and the approximations are measured in the corresponding norms. The networks are constructed explicitly. Because of the different methods of proof, the two results give independent insight into the approximation properties of random dropout networks. With this, we establish that dropout neural networks broadly satisfy a universal-approximation property.

Asymptotic convergence rate of Dropout on shallow linear neural networks

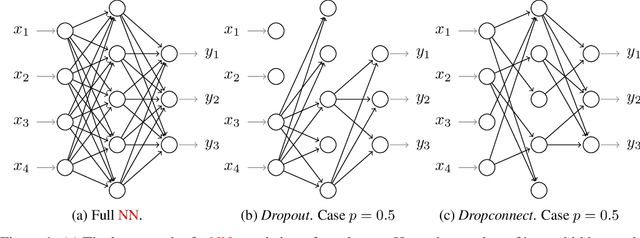
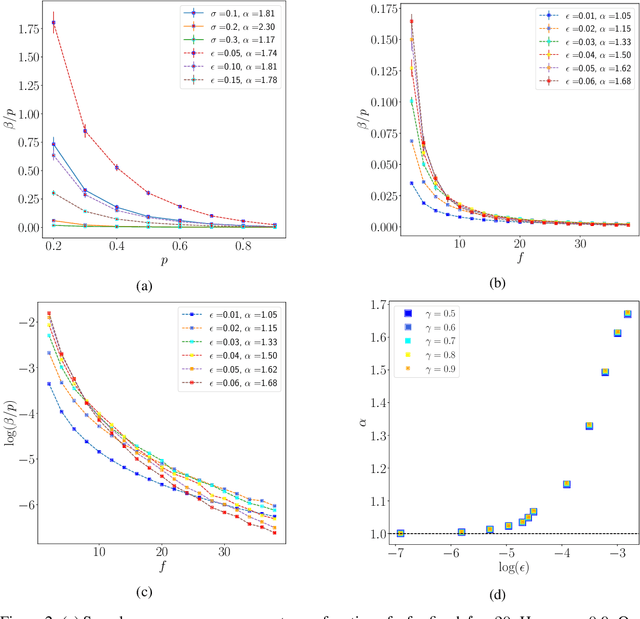
We analyze the convergence rate of gradient flows on objective functions induced by Dropout and Dropconnect, when applying them to shallow linear Neural Networks (NNs) - which can also be viewed as doing matrix factorization using a particular regularizer. Dropout algorithms such as these are thus regularization techniques that use 0,1-valued random variables to filter weights during training in order to avoid coadaptation of features. By leveraging a recent result on nonconvex optimization and conducting a careful analysis of the set of minimizers as well as the Hessian of the loss function, we are able to obtain (i) a local convergence proof of the gradient flow and (ii) a bound on the convergence rate that depends on the data, the dropout probability, and the width of the NN. Finally, we compare this theoretical bound to numerical simulations, which are in qualitative agreement with the convergence bound and match it when starting sufficiently close to a minimizer.

Almost Sure Convergence of Dropout Algorithms for Neural Networks

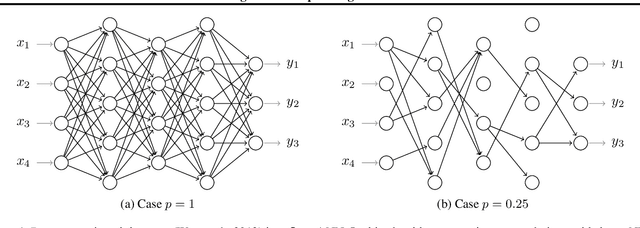
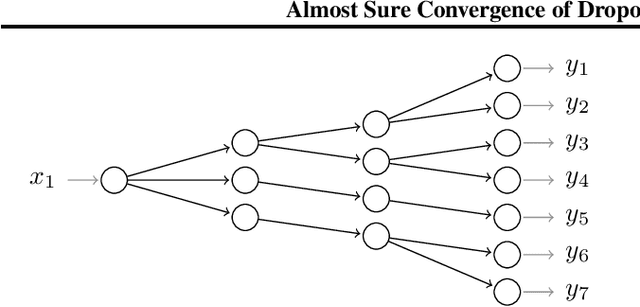
We investigate the convergence and convergence rate of stochastic training algorithms for Neural Networks (NNs) that, over the years, have spawned from Dropout (Hinton et al., 2012). Modeling that neurons in the brain may not fire, dropout algorithms consist in practice of multiplying the weight matrices of a NN component-wise by independently drawn random matrices with $\{0,1\}$-valued entries during each iteration of the Feedforward-Backpropagation algorithm. This paper presents a probability theoretical proof that for any NN topology and differentiable polynomially bounded activation functions, if we project the NN's weights into a compact set and use a dropout algorithm, then the weights converge to a unique stationary set of a projected system of Ordinary Differential Equations (ODEs). We also establish an upper bound on the rate of convergence of Gradient Descent (GD) on the limiting ODEs of dropout algorithms for arborescences (a class of trees) of arbitrary depth and with linear activation functions.