Noise-Resilient Designs for Optical Neural Networks

All analog signal processing is fundamentally subject to noise, and this is also the case in modern implementations of Optical Neural Networks (ONNs). Therefore, to mitigate noise in ONNs, we propose two designs that are constructed from a given, possibly trained, Neural Network (NN) that one wishes to implement. Both designs have the capability that the resulting ONNs gives outputs close to the desired NN. To establish the latter, we analyze the designs mathematically. Specifically, we investigate a probabilistic framework for the first design that establishes that the design is correct, i.e., for any feed-forward NN with Lipschitz continuous activation functions, an ONN can be constructed that produces output arbitrarily close to the original. ONNs constructed with the first design thus also inherit the universal approximation property of NNs. For the second design, we restrict the analysis to NNs with linear activation functions and characterize the ONNs' output distribution using exact formulas. Finally, we report on numerical experiments with LeNet ONNs that give insight into the number of components required in these designs for certain accuracy gains. We specifically study the effect of noise as a function of the depth of an ONN. The results indicate that in practice, adding just a few components in the manner of the first or the second design can already be expected to increase the accuracy of ONNs considerably.

Detection and Evaluation of Clusters within Sequential Data

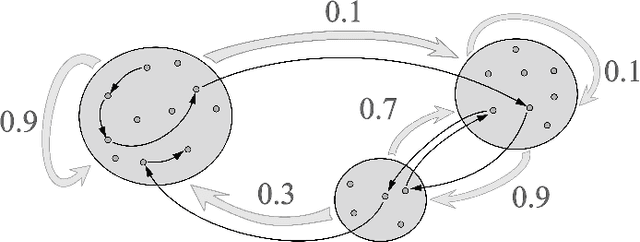
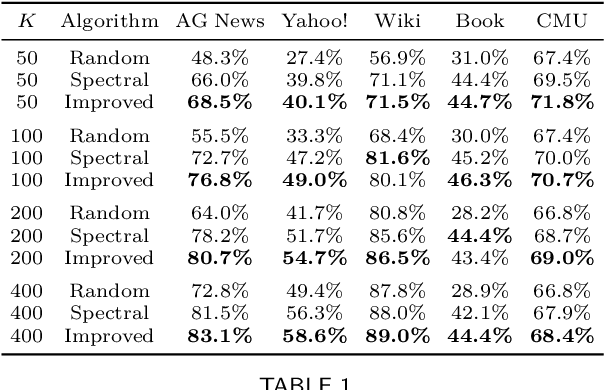
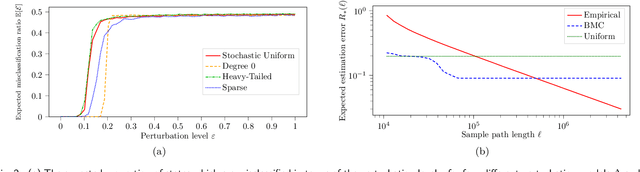
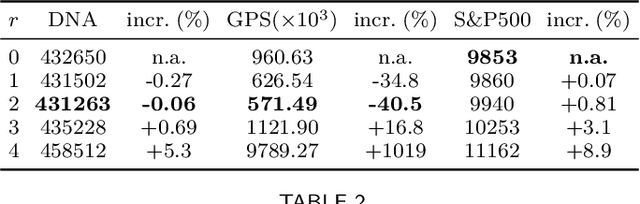
Motivated by theoretical advancements in dimensionality reduction techniques we use a recent model, called Block Markov Chains, to conduct a practical study of clustering in real-world sequential data. Clustering algorithms for Block Markov Chains possess theoretical optimality guarantees and can be deployed in sparse data regimes. Despite these favorable theoretical properties, a thorough evaluation of these algorithms in realistic settings has been lacking. We address this issue and investigate the suitability of these clustering algorithms in exploratory data analysis of real-world sequential data. In particular, our sequential data is derived from human DNA, written text, animal movement data and financial markets. In order to evaluate the determined clusters, and the associated Block Markov Chain model, we further develop a set of evaluation tools. These tools include benchmarking, spectral noise analysis and statistical model selection tools. An efficient implementation of the clustering algorithm and the new evaluation tools is made available together with this paper. Practical challenges associated to real-world data are encountered and discussed. It is ultimately found that the Block Markov Chain model assumption, together with the tools developed here, can indeed produce meaningful insights in exploratory data analyses despite the complexity and sparsity of real-world data.